Matematyka 2 A5

•114 VI Elementy statystyki mutemulyczncj

należą: średnia arytmetyczna próbki, wariancja próbki i odchylenie standardowe próbki.

Średnią arytmetyczną próbki (x,,x₂.....x₀) nazywamy liczbą x

określoną wzorem

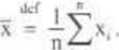
(3.1)

1=1

Gdy w próbce jest tylko k różnych elementów. k<n, z których pierwszy powtarza sic n, razy, drugi - n» razy , ... k-ty - n_k razy, to próbka taka daje sic opisać tabelą

^xi	*1	*2		*k
",	"l	"2	. ..	"k

_dc^f J

X ~

i średnią arytmetyczną takiej próbki można zapisać w postaci:

(3.2)

= -I",v

t-l

n| -f-n₂+n_k = n

Liczba x określona tym wzorem nazywa się średnią ary tmetyczną ważoną próbki, przy tym liczba n nazywa się wagą elementu x,. Zrozumiałe. że liczby określone wzorami (3.1) i (3.2) są równe.

Średnia arytmetyczna próbki w postaci szeregu rozdzielczego przyjmuje postać średniej arytmetycznej ważonej;

U

(3.3)    ^gdz,L'    !•*•&) ' środek i-tej klasy.

p|

Określenie (3.1.) można zapisać w po>taci x= > x,p₍. gdzie p, = =const = l/n Widać stąd, że średnią arytmetyczną próbki można traktować jako wartość oczekiwaną ZLS o rozkładzie równomiernym Zatem: średnia ary tmetyczna próbki ma wszystkie własności wartości oczekiwanej ZL W szczegóInuści:

(3.4)    £(x,-x)^0. x c+I^(x,-c),    x=a.i£i-.

t-l    «=l    ‘ 1-1

4. Za miarę rozrzutu próbki (x_|tx₂.....x_n) względem średniej aryt

metycznej x najczęściej przyjmuje się wariancję próbki s‘ opkreśloną wzorem:

(35)    s^: = ^-£(Xj-x)^:

i=i

lub odchylenie standardowe próbki: s=^. Wariancja próbki ma wszystkie w łasności wariancji 7.L. W szczególności:

i ⁿ    i

(3.6)    ł = -£(x, ~c)³ ~(c-x)‘\    r=-£xf-x^:.

i=i    i*i

Liczby e dobiera się lak. aby różnice x,-x były "wygodne" w dalszych obliczeniuch. Drugi wzór (3.6) wynika z pierwszego dla c=0.

ZADANIA DO ROZWIĄZANIA.

I. Z jakiej własności wariancji ZL wynika pierwszy wzór (3.6). Sprawdzić również jego prawdziwość bezpośrednim rachunkiem

2    Ze wzoru (3.6) wyznaczyć sumę ^T(x,-c)*. Dla jakiej wartości c suma la osiąga minimum?

3    Napisać wzory (3.5) i (3.6) dla wariancji próbki: 1) w klórej elementy powtarzają się oraz 2) w postaci szeregu rozdzielczego.

4. Zakład produkujący wyroby elektryczne otrzymał od kooperanta 140 elementów. Wyniki pomiaru oporności (w omach) u każdego z tych elementów zgrupowano w następujący szereg rozdzielczy:

54 50	S6-5X	58- 6U	60-02	02-64 1 64-06 1 06-08	6K-70 1 70- 72
2	X	17	23	39 1 20 | 16	9 1 6

Wyznaczyć: a) histogram, b) średnią arytmetyczną próbki, c) wariancję próbki

O (I |i o w I e d / I 2. c- \ ,

2) we watrach /. punktu I) lic/by x, zastąpić liczbami x, (środkami klas) 4 h» x-63,2; c) »² -12.99.