Matematyka 2 C5

434 VI. Elementy siary styki matemaryczjwj

I) Określamy statystykę testów;* U

(7.1)    Us^ZMł^

er

i obliczamy jej wartość u_tSlin dla danej' próbki (x_l,x_;„.„\_n). Zauważmy, że statystyka U mierzy "rozbieżność" (w tym przypadku różnicę) między wartości;! x statystyki X (X jest dobrym estymatorem wartości oczekiwanej (i) i wartością p, parametru \\ zadaną hipotezą H„; ponadto u-względnia znajomość odchylenia standardowego a

2)    Przy założeniu prawdziwości hipotezy H„(p = )J₀), statystyka <~ I) ma standaryzowany rozkłud normalny N(0.11 Wyniku to z definicji PI P i tw. 1.3. jeśli zauważyć, że przekształcenia po prawej sironic wzoru (7 1) stanowią standaryzowanie średniej arytmetycznej X

3)    Z tablic rozkładu N(0,l) odczytujemy kwantyI u₍__a i budujemy prawostronny zbiór krytyczny

(7.2)    K_u=<u_la,»).

a)    Jeśli u_m,_p eK._a, to na poziomie istotności u odrzucamy hipotezę zcruwąH ,(p=p„)na korzyść hipotezy alternatywnej H₍()i>óJ. Uzasadnienie tej decyzji znajdzie Czytelnik w końcowej części paragrafu 6

b)    Gdy u^eKy, to ograniczamy się do stwierdzenia dana próbka nic przeczy hipotezie ll₀(p = p„). (uzasadnienie - por. odp. do zadania 3 w paragrafie O)

Uzasadnimy jeszcze postać (⁷ 2) zbioru kry tycznego. Bierzemy tu prawostronny zbiór krytyczny, tj zbiór postaci K.., =< b,xj, ponieważ duże wartości u^ statysty ki testowej U świadczą przeciwko prawdziwości hipotezy H„m p„) » są jednocześnie argumentem za prawdziwością hipotezy alternatywnej H_il(p>p„), w potwierdzeniu prawdziwości której jesteśmy zuinleresowam Dlaczego b-u,.,,*.’ Otóż ze związku

(6.2) , w którym zakładamy znak rów ności, otrzymujemy

PtUcKjH,, jest prawdziw^ra) = P(l =<b,z-)ill₀ jest prawdziwa ) =

= P(U>b|ll, jest prawdziwą ) = a

Stąd

P(U<b|H„ jest prawdziwa)-l-a.

Z założenia, że II₀ jest prawdziwa wynika, że statystyka U ma rozkład normalny N(0,l). Stąd i z ostatniej równości otrzymujemy, że b jest kwantylem rządu p = 1-a ZL U o rozkładzie N(O_tl): b= u,.^.

PRZYKI.AD 7.1. Według normy przeciętny czas wykonania danego detalu wynosi 28 godzin. Pracownicy wyrażali obawę, że czas ten jest większy. Dokonano pomiaru czasu wykonania 15 detali otrzymując wyniki x, 27, 30. 27. 31, 29. 31, 27. 31. 29. 31. 29, 31. 27. 31), 28. Zakładając, żc wyniki te są wartościami ZL X o rozkładzie normalnym N(p;1.7) zbadamy, czy przypuszczenia pracowników o zaniżeniu normy dadzą się potwierdzić statystycznie.

Czas wykonania.detalu według normy uważamy za hipotezę zerową Il₍₁(p=28). a wysuwane obawy pracowników o zaniżeniu normy czynimy treścią hipotezy alternatywnej H_J(p>28) Obieramy poziom i* stotności u =0,02 Warunki zadania czynią zadość warunkom W’! Stosujemy omówiony wyżej test

I) Statystyka testowa jest postaci (7.1). Dla danej próbki obliczamy jej wartość empiryczną, czyli u^ :

Ponieważ

więc

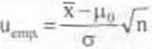
. I £    ,o. I

*⁼bI^x'⁼²⁸⁺ttI^(x<-^2X>^=2k+ti^,8=2‘^j-^{1 2}’

1=1    Ńl

•emu

₌ 29^_2K^ _{= 273}

1

   Statystyka U określona równością (7 1), przy założeniu prawdziwości hipotezy H„(p = 28) ma rozkład normalny N(0.l).

2

   Z tablic kwantyli tego rozkładu odczytujemy kwantyI _U|__ii = u,_wl = 2.05 i budujemy prawostronny (dlaczego) zbiór krytyczny

(por. rys 7.1)

K_ou2 = <2,05; cr.).

Ponieważ =2.73 sK.„,_i2 =<2,05;*). więc na poziomie istotności a = 0,02 odrzucamy hipotezę zerową H„(p = 28) na korzyść hipotezy alternatywnej ll₄(p>28) orzekającej, że przeciętna czasochłonność wy-