Matematyka 2 @9

408 VI. Elementy stuły styki matematycznej
Teoretycznego wyjaśnienia zasadności takiego postępowania dostarczają centralne twierdzenia graniczne (CTti) rachunku pr-stwa. Tak nazywa się twierdzenia, które orzekają o zbieżności rozkładu sum zmiennych losowych do rozkładu normalnego, gdy liczba składników dąży do nieskończoności. Zacytujmy jedno z najprostszych takich twierdzeń i przypadek szczególny tego twierdzenia.
TWIERDZENIE 2.5 (CTG Lindebcrga-Levy*cgo). Jeżeli ZL
X|.X2.....są niezależne, mają ten sam ro/kład pr-stwa, skończoną
wartość oczekiwaną p = F.X,. skończoną i różną od zera wariancję a2 = VarX,, to ciąg dyslrybuunt (hn) standaryzowanych ZL Un
(2.5) u> = sŁ-mii gd2jc s,»X1+XJ+...+X11
avn
jesl zbieżny na całej prostej do dystrybuant} <I> standaryzowanego rozkładu normalnego N(0,l):
t I z
(2.6) lim E„(u)=0(u). czyli lim P(Un <u)=-= fe dt.
nn-ł'jo v2tt ^
Z (2.6) wynika również, że
I “f • łi*
(2.7) lira P(U| <U„ <uv)=-p= c - dt=d>(u .)— <X>(u;).
ui
Dla dużych n / (2.6) i (2.7) wynikają następujące przybliżenia normalne dla standaryzowanych sum U„
ctg cni
(2.8) P(UM <u) * d>iu). Pi u, <Un<u:) = <t>(u:)-<I>(u,)
PR Z Y K ł AD 2.2. Każdą zc 192 liczb z dużą ilością cyfr po przecinku zaokrąglamy do części całkowitej Przyjmujemy, ze błąd zaokrąglenia X, i-tej liczby. i = 1.2.....192. jest ZL o rozkładzie prostokątnym R(-0.5;0.5). Interesujący nas błąd sumy tych 192 liczb jest wówczas ZL postaci S,g2 =Xj + X:+...^X|92. Obliczymy pr-stwo, żc błąd ten co do modułu będzie mniejszy od 10: P(|SI0?|< 10).
Posłużymy się przybliżeniem (2.8). Korzystając zc wzorów na wartość oczekiwaną i wariancję ZL o rozkładzie prostokątnym R(a,b), otrzymujemy:
EX, = j(a + b) = 0, VarX,=-^(b-ur = -^
c _icn.n c
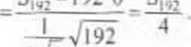
Zatem według (2.8) mamy:
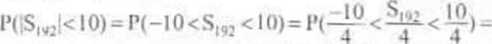
5 <l>(25)- <t>( - 2,5) = 2<J»( 2,5)-1 = 2 0.9938 -1 = 0.9876 * 0,99 Szukane pr-stwo w przybliżeniu wynosi 0.99 Na zakończenie przypomnijmy, że zgodnie z teorią błędów, maksymalny bezwzględny błąd sumy jest równy sumie maksymalnych błędów bezwzględnych składników. W rozważanym przykładzie należałoby zatem przyjąć, że jest on równy 192*0,5=96. •
Z ostatniego tw ierdzenia - jeśli uwzględnić równość (5.3) z rozdziału V oraz równości ES, = np, VurS„ =npq. DS„ - ^nptj - wynika
TWIERDZENIE 2.6 (Moivre'a - Laplace'a) Jeżeli (Sn) jest ciągiem 7.L o rozkładach dwumianowych b(n,p), to ciąg dystrybuant (Fn) standaryzowanych Zł Un.
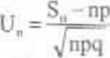
jest prz> ii->t zbieżny na całej prostej do dystrybuanty <6 standaryzowanego rozkładu normalnego N(0;l):
(2.10) P(UM<u) a F,(u)-mIKu), ueR
Prawdziwe są również przybliżenia postaci (2.8).
PRZYKŁAD 2.3. Pr-stwo. że klient domu handlowego poszukuje ubrania o danym rozmiarze wynosi 0,2. Znajdziemy pr-stwo tego, że wśród 1500 kupujących liczba S,500 tych, dla który cli w łaściwy jest dany rozmiar, zawierać się będzie w przedziale (280; 330).
Wielkość S,„, test Zł. o rozkładzie dwumianowym b( 1500;0.2). Poszukiwane pr-stwo znajdujemy na podstawie twierdzenia Moivre’a -Lapłace‘a i wynikającego z niego przybliżenia postaci (2.8):
P(2X0<Sl5O(l<330)- P(
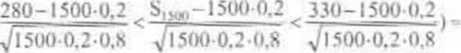
Wyszukiwarka
Podobne podstrony:
Matematyka 2 C5 434 VI. Elementy siary styki matemaryczjwj I) Określamy statystykę testów;* U (7.1)
Matematyka 2 @1 400 VI. Elementy statystyki matematycznej ma lę samą wartość oczekiwaną co składnik
Matematyka 2 @3 402 VI riemctuy staty styki nmtamatytzjiej Pr-siwu lego. że średnia arytmetyczna X2
Matematyka 2 @5 404 VI. Elementy statynyki muiemutycznej Z symetrii względem osi Oy krzywej gęstośc
Matematyka 2 @7 406 VI Elementy . ui sn ki malcmuiyrzncj Prawo to orzeka, że pr-slwo odchylenia (co
Matematyka 2 A5 •114 VI Elementy statystyki mutemulyczncj należą: średnia arytmetyczna próbki, wari
Matematyka 2 A9 418 VI Elementy stutysh ki mairmaiu znef ^I-X
Matematyka 2 B3 422 VI. Elementy iuiysiyki niaic/nulu znrj Gdy dysponujemy próbką (x,.x2.....x0) ce
Matematyka 2 C3 432 VI Elementy statystyki ntuicntut mt j trafnej decyzji) Rozważane dalej testy, t
Matematyka 2 C7 436 VI Elementy statystyki matcmutyyznet konania jednego detalu jest większa od 28
Matematyka 2 C9 43S VI. Elementy siaiyuykt matematycznej 2) Przy założeniu prawdz
Matematyka 2 D3 442 VI Elementy statystyki maicmatwznej_ 2) Z tablic rozkład chi-
Matematyka 2 D5 444_VI. Elementy statystyki matematycznej_ 5. Dla danych z zadani
Opis studiów Studiując specjalność MATEMATYKA TEORETYCZNA zdobywasz wiedzę z wszystkich podstawowych
EGZAMIN MAGISTERSKI, 18.09.2012 Matematyka teoretyczna Zadanie X • (8 punktów) Znajdź rozkłady
Jarosław Wróblewski Matematyka Elementarna, zima 2013/14 Wzory skróconego mnożenia, procenty, postęp
VI. Przebieg ćwiczenia a) Sprawdzić przygotowanie teoretyczne studentów do ćwiczen
SNV36487 VI. Element okultystyczny w ideologii masońskiej "Istnieje w masonerii tajna doktryna
^/EBMiR:pt^Vi Elementy Budowy Maszyn i AutomatykiKlej do metalu -jaki kupić? Y
więcej podobnych podstron