Matematyka 2 @5

404 VI. Elementy statynyki muiemutycznej

Z symetrii względem osi Oy krzywej gęstości Studenta wynika, ze podobnie jak dla ZL U o rozkładzie \(0*l). kwantyle ZL t₄ o rozkła-dzie Studenta spełniają warunek:

404 VI. Elementy statynyki muiemutycznej

PRZYKŁAD 1.3. ZL X ma rozkład Studenta 7 k = 12 stopniami swobody Chcemy znaleźć liczbę x spełniającą warunek: P(X<x) = U.l.

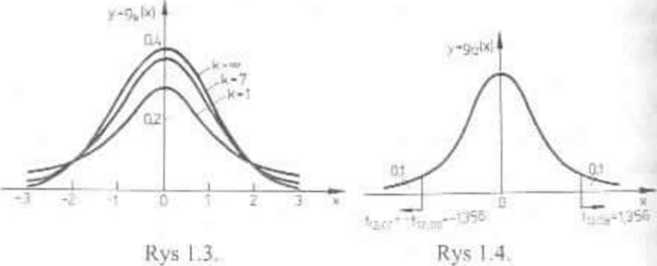
Mamy: P(X<x)= P(t_l2<x)=0,l. Szukaną liczbą jest więc kwantyl    Tablica II kwantyli rozkładu Studenta zawiera tylko

kwantyle rzędu p>0,9 Pomocna jest tu równość (17). (rys 14):

I|2;0.l^=-tl2;6.0 ⁼ “135fi    łfl

Wartość oczekiwana 1 wariancja ZL t_k o rozkładzie Studenta z k stopniami swobody wyrażają się w/orami (Et^ istnieje dla k> 1. Varl_k istnieje dla k >2).

(1.8)    Et_k=0, Vart_k = k/(k-2).

Związek rozkładu Studenta z rozkładem normalnym 1 sens liczby stopni wynika / następującego twierdzenia.

TWIERDZENIE 1.6 Jeżeli. I) ZI. U i Y są niezależne. 2) ZL U ma rozkład normalny N(0;l), 3) 7.L Y ma rozkład chi-kwadrat / k stopniami swobody, to ZL Z

ma rozkład Studenta z k stopniami swobody.

Zastosowanie rozkładu Studenta poznamy w paragrafach 5 1 7.

ZADANIA DO ROZWIĄZANI A.

1    ZL X,,X_:.....X_l6 sit niezależne i mają ten sam rozkład normalny

N(l,2); S₎₀ i oznaczają ich sumę i średnią arytmetyczną. Obliczyć:    a) P(|S,*-I6|<8), b) P(|X_W-I|<1).

2    ZL X,.X_:.....X_l0 są niezależne i mają ten sam rozkład N(0;1). Wyz

naczyć liczbę a spełniającą warunek P(Xf -X;+*-*+Xf_u <a)=0,95

3    ZL X,.X₂.....X, są niezależne i mają ten sam rozkład normalny

N(0;l) Wyznaczyć liczbę a spełniającą warunek

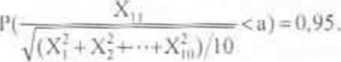
O i) |i o w I c d z i . I. aiO.fiS; hjU.95.    2s=IK.3t. J a = !.XI2.

2. PRZYKŁADY TWIERDZEŃ GRANICZNYCH

W paragrafie 5 rozdziału V poznaliśmy twierdzenie o zbieżności ciągu rozkładów dwumianowych do rozkładu Poissona. Jest to przykład twierdzenia granicznego. Twierdzenia graniczne są ważnym działem rachunku pr-stwa i stanowią podstawę wielu procedur statystycznych. O-becnic sformułujemy najprostsze, klasyczne przykłady takich twierdzeń.

Sł.ABF PRAWA WIELKICH LICZB

TWIERDZENIE 2 I (słabe prawo wielkich liczb Chinczyna) Jeżeli

X,,X_:.....X_n%... jest ciągiem niezależnych ZI o jednakowym rozkładzie

pr-stwa i skończonej wartości oczekiwanej HX - p, to przy dowolnym E > 0 I n-»ao

(2 1)

P(|X_łt-M|<E)->l.

gd/ie X_p oznacza średnią arytmetyczną ZL X,.\\,...,X_h.