51941 MATEMATYKA175

340 VI Ciągi i szeregi funkcyjne

równości iz oraz -iz zamiast z otrzymujemy

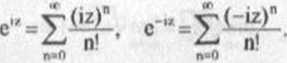
Stąd wynikają następujące związki między funkcjami e' ,cosz, sin z nazywane wzorami Eulera (por. rozdz. I, 2):

cosz=“(e^,r+e'^,ł)_t sinz= Jr(e“-e*), e'^l=co$z+isinz.

ZADANIA DO ROZWIĄZANIA

1.    Obliczyć granicę ciągu (z¹).

2.    Czy ciąg (zⁿ) jest jednostajnie zbieżny do funkcji f(z)=0 na zbiorze D={zeC: |z|<a<l}?

3. Czy ciąg (zⁿ) jest jednostajnie zbieżny na zbiorze D = {z eC: |zj< 1} ?

4.    Obliczyć promień zbieżności szeregów:

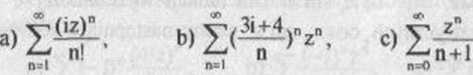
5

Obliczyć sumę	szeregu i znaleźć zbiór tych z eC, dla których jest on
zbieżny:
a) £(z-2)\	b) £<z-2)\	c) £(2-0".
n»l		n 1
^d> n 0	n 1	oi>-\ m(l

"• /_Ailm7.\n

*>    7.n

Wyznaczyć zbiór tych zeC. dla który ch zbieżny jest szereg:

" /JRcZvl»

7. Stosując kryterium Weicrslrassa wykazać zbieżność jednostajną szeregu na podanym zbiorze:

a) jTz" dla |z|£a. 0< a < 1, b) dla |zjsl,

n-0    B»l ⁿ

c) £^dla |zj^a. a >0, d) ^T^fdla |z(ia. a > 3.

Odpowiedzi.

1.    0 dla łzj>1, l dla z=l. mc istnieje dla |z|sl i2#l.

2.    Tak

3.    Nie.

4.    a) r=+oo, szereg zbieżny dla wszy stkich z, b) r=+*>. c) r= 1, szereg zbieżny dla |z|< 1, rozbieżny dla |zj> 1.

5.    a) ~=- , szereg zbieżny jedynie dla |z-2|< 1 tzn. wewnątrz, okręgu o środku (2,0) i

promieniu 1, b) ,|z-2J<l, c)-p^-, |z-i|<! tzn wewnątrz okręgu o środku (0,1) i promieniu 1 , d) Z-ł-1, Rcz>--^, c)-•^(zi+l)_>lmz>0.

6.    a) Dla wszystkich z; le^,RM|He^łXheosx+isinx|- cos² x+sin² x-1,

|<^elRe/jl ₌-L, yJ_ /bieżny, więc badany szereg jest jednostajnie zbieżny dla n² n² n²

wszystkich ZcC, b) dla wszystkich zeC, c) Ke/50