011(1)

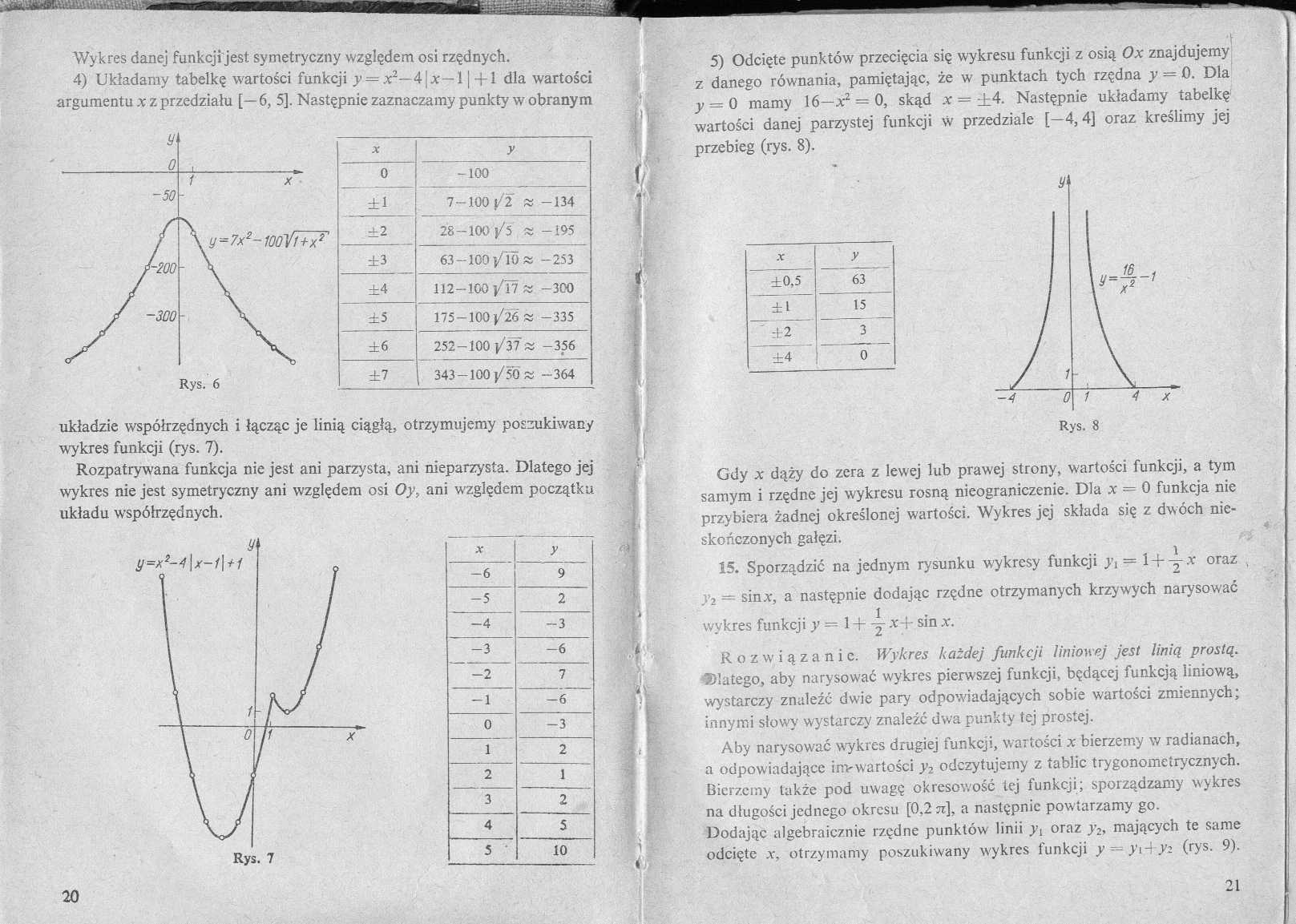
Wykres danej funkcji jest symetryczny względem osi rzędnych.

4) Układamy tabelkę wartości funkcji y = x²—4\x—11 +1 dla wartości argumentu x z przedziału [— 6, 5], Następnie zaznaczamy punkty w obranym

X	y
0	-100
±i	7—100 [/l x -134
±2	28-100 j/5 X -195
±3	63-100 {/TO « -253
±4	112-100^17 X -300
i5	175-100^26 ss -335
±6	252—100 x -356
±7	343 — 100 j/50 X -364

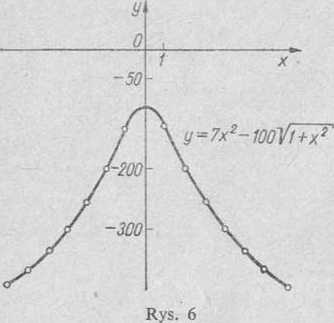
układzie współrzędnych i łącząc je linią ciągłą, otrzymujemy poszukiwany wykres funkcji (rys. 7).

Rozpatrywana funkcja nie jest ani parzysta, ani nieparzysta. Dlatego jej wykres nie jest symetryczny ani względem osi Oy, ani względem początku układu współrzędnych.

X	y
-6	9
-5	2
-4	-3
-3	-6
-2	7
-1	-6
0	-3
1	2
2	1
3	2
4	5
5	10

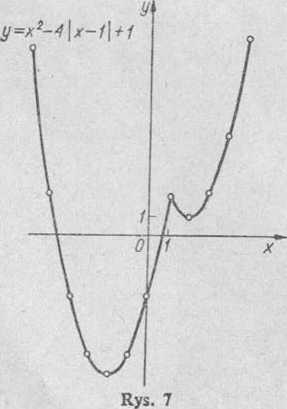
5) Odcięte punktów przecięcia się wykresu funkcji z osią 0x znajdujemy z danego równania, pamiętając, że w punktach tych rzędna y — 0. Dła y = 0 mamy 16—*² = 0, skąd x = ±4. Następnie układamy tabelkę wartości danej parzystej funkcji W przedziale [—4,4] oraz kreślimy jej przebieg (rys. 8).

X	y
±0,5	63
±1	15
±2	3
±4	0

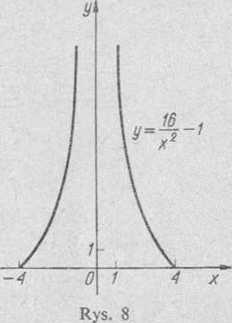
Gdy x dąży do zera z lewej lub prawej strony, wartości funkcji, a tym samym i rzędne jej wykresu rosną nieograniczenie. Dla * = 0 funkcja nie przybiera żadnej określonej wartości. Wykres jej składa się z dwóch nieskończonych gałęzi.

15. Sporządzić na jednym rysunku wykresy funkcji p_t = l + ^-.r oraz , ₂ = sin*, a następnie dodając rzędne otrzymanych krzywych narysować wykres funkcji y — 1 + y *+ sin x.

Rozwiązanie. Wykres każdej funkcji liniowej jest linią prostą. ^Dlatego, aby narysować wykres pierwszej funkcji, będącej funkcją liniową, wystarczy znaleźć dwie pary odpowiadających sobie wartości zmiennych; innymi słowy wystarczy znaleźć dwa punkty tej prostej.

Aby narysować wykres drugiej funkcji, wartości * bierzemy w radianach, a odpowiadające invwartości y₂ odczytujemy z tablic trygonometrycznych. Bierzemy także pod uwagę okresowość tej funkcji; sporządzamy wykres na długości jednego okresu [0,2 zr], a następnie powtarzamy go.

Dodając algebraicznie rzędne punktów linii p, oraz y₂, mających te same odcięte *, otrzymamy poszukiwany wykres funkcji p — pH yz (rys. 9).

21