MATEMATYKA027

j) y = l + arctgx, k) y = arcsin2x, 1) y = arccos(cosx).

4 Naszkicować wykres danej funkcji, a następnie podać przedziały, w których ta funkcja jest róźnowartościowa: a) y = x² -3x, b)y = log,x, c)y = ctgx.

j

5.    Wykazać, że funkcja

x²-l

a) y = x - x², b) y = sinx, c)y = 3^2W, d)y = -j—

X “ł t

nic jest róźnowartościowa na zbiorze R

6.    Naszkicować wykres danej funkcji i wskazać przedziały, w których funkcja ta jest ściśle monotoniczna:

a) y = 3-2x-x², b)y = 2cosx, c)y = ctgx,

fx^;+2x + l, x < — 1,	j 4 - x^2, x < 0,
^ć)y={ 2 „ o	^e)y =
lx“-2x-3, x£-l.	[ x + l, x>0.
Wykazać, że funkcja
a) y = tgx, b) y = x + x^2,	c) y = 2‘^RI, d) y = x|x + 2'

nie jest rosnąca w całej swojej dziedzinie.

Naszkicować wykres funkcji ² x <0, x £0,

a) y =

_b) y={,^x2_1,

llOgr,,X.

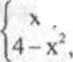
x£l.

X > 1,

a następnie wy kazać, źc nie jest to funkcja malejąca na zbiorze R.

9. Narysować wykres funkcji określonej na zbiorze R. różnowartościo-wcj. ałe nic monotoniczncj.

10.    Zbudować funkcję złożoną F(x) - f(g(x)), gdy

a) f(x) = x² -2x, g(x) = cosx, b)f(x) = logx, g(x) = 2 + 3\

11.    Wyznaczyć funkcję f ¹ odw rotną do funkcji f. gdy

a)f(x) = 2x-l, xeR.    b) f(x) = x^J -1, x€(-oo,0>,

c)f(x) = 3", xgR,    d)f(x) = —, xgR-{0},

x

c) f(x) = log₁(x + 2)_ł x€(-2,+x), Of(x)=x\ x gR, a następnie naszkicować wykresy funkcji y = f(x) i y = f' (x)

fN

x

Wykazać, żc funkcja y =-jest różno wartościowa w swojej dzic-

x +1

dżinie, a następnie wyznaczyć funkcję odwrotną do niej.

13 Obliczyć:

a)    aresin 1 - 2 arccosO -t- 3arctg(-1),

b)    arcctgO + arctg(->/3) - aresin -,

c)    aresin(- —) - 3arctgV3 + 4arcctg 1,

d) aresin (sin    + aresin (sin ^7t).

o    o

14. Wśród podanych niżej funkcji wymiernych wskazać ulainki proste 1 i U typu:

x²-l    .. x + l    .    2

a) y = d) y =

x-3

x

^b)y=

x +4 5

e)y = -i-

c) y =

0 y =

x³ + f 1

(x — l)² ’    x²-x + 3’    (x-3y

15. Rozłożyć na ułamki proste następujące funkcje wymierne:

5-x    x²+3x + 3    4

^a)y”x²+2x-3’ ^y x' + 2x² + x ’ ^Cy X¹ + 4x

Odpowiedzi.

2 d)(-.VlM2,+«),    b)(-2,-!M-1.2>, c) (-2,-1), d)<-l,0>,

e)(0.1M1,+oo),    0(~».-IM2,-wo), g) (-00,1), h)<-l,4oo).

5. Wsk Wystarczy wskazać dwa różne punkty x,.x₂ «R. dln których y(x,)»y(x₂).

7. Wsk. Wystarczy wskazał dwa punkty x, < x_: z dzicdzinv, dla których y(x, )> y(x₂). 8 Wsk Wystarczy wskazać dwa punkty x, <x, z dziedziny, dla których y(x,) < y(x₂) 10. a) l•'(x)“c<Ml²x-2coJx, xeR b) F(x)- 108(2+3*), xeR.