89061 MATEMATYKA172

334 VI. Ciągi i szeregi funkcyjne

a następnie naszkicować wykres sumy S(x) otrzymanego szeregu na przedziale <-2k,3k>,

2.

Rozwinąć funkcję f w szereg Fouriera i naszkicować wykres sumy S(x) otrzymanego szeregu na przcdzjale < -4,4 >:

c) f(x) =

fx dla x€(-2,0), (0 d!axec0,2)

a) f(x)=x dla xe( 2,2),

x+2 dla x e(-2,0), x dla x 6(0,2),

b) f(x) =|xj dla x€<-2,2>,

d) f(x)=

3,

Rozwinąć funkcję I* w szereg Fouriera i naszkicować wykres sumy S(x) otrzymanego szeregu na przedziale <-2rr,37c>. Obliczyć S(0), S(l), S(37t):

x *-2it dla X€(-K,0), x dla x€(0,n),

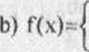
x dla xe(-7r,0), \-2n dla xe(0,rt)

4. Rozwinąć funkcję f w szereg Fouriera według sinusów:

a) f(x)=xdlaxe<0_T7r),    b) f(x)=xdla xe(-ir,0>,

c) f(x)=l-xdlaxe(0,7t),    d) f(x)=2xdla xe<0,2)

5. Rozwinąć funkcję f w szereg Fouriera według cosinusów:

a) f(x)=x dla xec0,7t>,    b) f(x) = x dla xe<-7t,0>,

c)f(x) = l-x dla xe<0,x>, d) f(x) = 2x dla xe<0,2>. Odpowiedzi.

<r.    j    ^    2 f    ą

1. a) x» V(-l)ⁿ"—«nnx,x«(-x,x), b) x²*-r-    -l)⁰---cosnx,x€<-ir,ic>,

o i    ^n    3 n i n

^ j * i

c)    |Rinxl=~~—cos2»x.x€<-x.n>,

% |4u -1

"> 4 ^u    1

d)    |cosx|«~~~ TH)" 7y--cos2nx. x « -x, nr >,

x ⁿ„ ij    4n -l

•y    j    |

c) I(x)a4+(%iiix —cosx)- ‘ sir)2x+(-Jsin3\ -^-C<»s3x)4-- dln x«(-jc,x),

f) f(x)- j-    *^,nX“f^COix)“2^%iP2X*

■H-r—sm3x-“"-cos3x)+..., xe(-x,0)u(0,k).

8) l'(x)*~+£(--~((>-l)ⁿ-l)co_:<nx-(-l)ⁿ^.Mnnx), xe (-x.il),

n=l 2xn

h) t'(x)=—+T(—~(l-(-l)ⁿ)cosnx-<-!)"-Uinnx), xe(-x,ii).

⁴ na| JOT    ⁿ

o ^f<*>4^łiśi“T^c“^nx'H ^

n I

X«<-lt,yMy4)^u(f*>'

j)    f(x)-^+~£-V(«>s™-(-0^c©mx. xg<-x,ic>,

⁸ *nr₍n‘

k)    f(x)a-+£(-^l-(-l>'‘)co«nioc-(-l)^,'-^-»inn»c), x«(-U),

⁴ _n | n‘ir    ⁷¹¹¹

1    *

l)    I'(x)=l~-co$xf2£~r—conx, xe<-jt,*».

²    n=2 M-l

2.    a)x=i£(-l)^{n l}^in-2^, xe(-2,2),

b) M*l--rS-i—COsĄt^ł-xx, xe<-2,2>,

*²nt₀(2n+l)²    2

•? * l

c)    f(x)= 1 — £—sinnxx, xe(-2,0)w(0,2),

*n Iⁿ

d) f(x) =-^+^(^cos-^+sin “)--Uin    •j^(-^cos-^+sin-^p)+... ,x €(-2,2).

3.    a) f(x)=x-2£—sinnx, x€(-n,0)u(0,x), S(0)=x, S(l)=l, S(3ic)=x,

n iⁿ

b)    f(x)»-x-2£—siimx, xe(-ir.0)w(0.Jt), JS(0)«-x, $(1)*1-2ji, S(3*)--*.

n I¹¹

4.    a) x=2£(-l)^n,,-Uinnx,x€<0.x). b) x-2£(-l)^'^»innx,x€(-x,0>,

n I    ⁿ    n*l    "

c)    1-_X,~^»inx-f|«in2x->^^i»in3x-f.... x«(0,x),

d> 2x-|£(-ir^l-i»in22Ł,x«0J).

”#■1

5.    _a) x=|^£^((-l)ⁿ-l)cosnx=|~£^-~_fcos(2n-_ł-l)x.x€<0.x>,

b) x =—--£ -U(- l)ⁿ -1 )cosnx*-* +~ £ —^-_Tco.><2n+l)x, x e< - x.0>,

²    *£>n^2    2    *rt=o(2n+l)²