2 (847)

Obszar D jest normalny względem osi Qx , zatem

-a<x<a

D = Ux,y)\

2

■2 >

■bJl—jśyśb Jl-^

V a~ v

)

Szukana objętość połowy bryły ograniczonej elipsoidą wynosi

i i

V -

D

X“ V .    ₇

CJi---~^~yrdxav

V a- b-

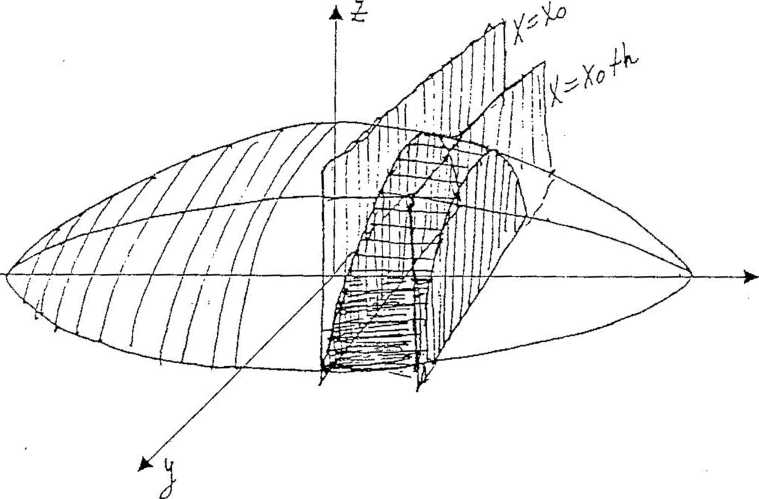
Wprowadźmy teraz dwie funkcje :    V(x) i S(x) takie, że

H*_n) oznacza objętość bryły zawartą między płaszczyznami

X = X,

S(x_Q) oznacza pole przekroju połowy elipsoidy płaszczyzną X — X^ zatem S^Cl') = S(~Cl') — 0 .

X*

Rozpatrzmy teraz przekroje bryły⁷ płaszczyznami X —X^, i X — X^ + h

Odpowiednie pola przekrojów będą równe 5^T(Xq) i S(_KXą^Jrh') zaś objętość części bryły zawartej między tymi płaszczyznami jest równa

A V = V(x₀+h)-V(x₀)    ■