2711906634

18 -

Wskutek symetrji belki i jej obciążenia względem osi    mamy:

A' = B*

a zatem:    *

2A¹ + C^ł = 2q/

C* -2q/-2A'=2q^-2. q/

8

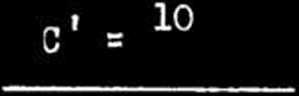
Sprawdzenie wartości C¹ zaporaocą sumy momentów względem punktu /b/

skąd:	8^
a zatem:	C^T =

2/- q/. 1/ + C'/ - q/ . Ć= 0

2 2

- q/² - 2q / + C'/ = 0

C' * / 2 - -/q/

c' " — q

8

l

Reakcje podpór belki są:

8

^c'

Siły tnące w belce.

Pierwsze przęsło. Wzór na siłę tnącą w przekroju w odległości /x^/ od

*

lewej podpory /a/ jest :

V/_x/ = A' - qx₁

Siła poprzeczna otrzymuje wartość równą zeru przy X]_ =    ^

V/ /s A¹ - qx/ ^    * 0

/x,o,v/    ^ /t|0,V/

£q/-

= 0

skąd:

Dla x, s / - ^x, , gdzie ^ix, jest to nieskończenie mała wielkość czyli w przekroju położonym nieskończenie blizko od podpory C, ale z lewej jej strony,

siła tnąoa przedstawia się następującym wzorem:

^T//W = %

Drugie przęsło. Wzór na siłę tnącą w przekroju w odległości xg wprawo od podpory Cj przedstawia się następująco:

^v/x_z/ = ^A' - q/ + ^c! - q^x2³ f q^ - q^ + — q^- q*2