27 (46)

t

t

59 Obszar normalny względem osi OX:

Ł-. Dx = {(x,y)eft²: a < x < b a <p(x) < y < \|/(x)}.

b ^

Obliczanie całki podwójnej

X - uI-o.

y yo ’■<. O cl    )C

p-yc* t.<A_ ±    @ y yy Y ja.

p^tc^ąc &l_brĆLv *, urn* X

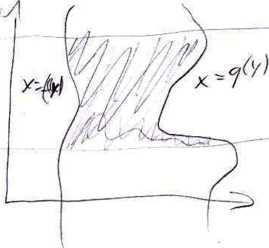
B Obszar normalny względem osi OY:

D_y = {(x,y)e!R²: c < y < d a f(y) < x < g(y)}.

W, l/ęZcL^c ty

X -> -rSr^e y<

Twierdzenie 5 (o zamianie całki podwójnej na całki iterowane).

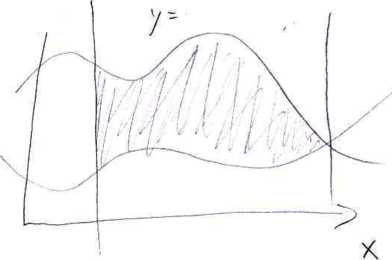
Jeżeli funkcja f: D-»9t jest ciągła w obszarze D c$R² normalnym względem osi OX:

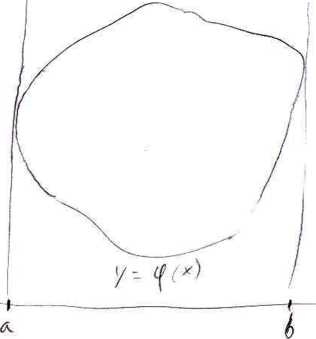
D= {(x,y)e$R²: a < x < b a cp(x) < y < \|/(x)}, to    ^

ip(x)

|f(x,y)dy

9(x)

b ip(x)

dx = Jdx Jf(x,y)dy.

a cp(x)

b

jjf(x,y)dxdy = J

/<d<-    / M-C-(9 Y

C & Ł a j ćmy oLĄ/p^ay^- po j/

< U A. C    ^ *

MAT2 Mechatronika Jan Nawrocki 27