200

398 XX. Zastosowania geometryczne całek

Rozwiązanie. Moment bezwładności łuku krzywej względem osi Ox znajdą ze wzoru (20.4.1). W danym zadaniu mamy y=(a^2,3 — x²¹³)³¹². Stąd

Obliczamy różniczkę łuku krzywej

‘^,L=V^1+:

dx= —r dx.

Teraz obliczamy poszukiwany moment bezwładności

a    a

I_x= f k (a^ł-x^ł)³ a^ł dx=Xaⁱ J (u² x~ⁱ-3a* x^ł + 3a^ł x-x^l)dx=

0    o

= Aa* [§ a² x^ł—| a*x-^ł+5 a^ł x²-| x^ł]ó = | Au³.

Zadanie 20.91. Deska o długości / zamocowana z jednej strony, została pokryta równomiernie śniegiem. Ciężar śniegu przypadający na jednostkę długości deski wynosi p. Obliczyć całkowity moment zginający deskę, wywołany ciężarem śniegu (rys. 20.12).

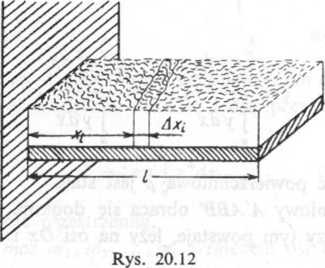
Rozwiązanie. Ciężar śniegu obciążającego deskę na długości Ax wynosi AP=pdx. Moment wywołany tym ciężarem wynosi AM=xp Ax. Całkowity moment wywołań) ciężarem śniegu wynosi

R    i    i

M= lim Yj px_iAx_i— ^ px dx=p \ x dx=p[jX²J₀ = ^pl². dx<->0i=l    o    o

Zadanie 20.92. Obliczyć moment bezwładności łuku cykloidy x = a(t—sin l), 3'" =u(l— cos/)> a>0, 0$/<2jr, względem osi Ox zakładając, że gęstość liniowa A j¹--¹ stała.

Rozwiązanie. Wiemy, że dla cykloidy dL — 2a sin \t dt (por. zad. 20.25). Mn¹¹¹' więc

^ 1 -cos / = 2sin² \t. Aby obliczyć całkę nieoznaczoną, wykonujemy podstawienie

• ' «/==(/, skąd — 4 sin \t dt = du, czyli sin \t dt = — 2 du. Mamy więc _L-os 5*

j sin⁵ ji dt = J (1-cos² \t)² sin \t dt= — 2 J (1 - u²)² du= -2 J (l-2u² +u⁴) du =

= -2 (u-§u³ +|u⁵) = -2 (cos \l-1 cos³ i-t+i cos⁵ ±t)-

Korzystając z tego wyniku otrzymujemy l_f = 8/ta³( - 2) [cos ij-§ cos³ łf+± cos⁵ ±f]oⁿ = — 16Aa³((—1+§ —|) —(1 -§+•;))

po redukcji ostatecznie otrzymujemy I_x-~Xa³.

Zadanie 20.93. Długi zbiornik w kształcie prostopadłościanu napełniony jest wodą jo wysokości h. Obliczyć moment M przypadający na jednostkę długości zbiornika, wywołany ciśnieniem p wody, dążący do odgięcia ścianki bocznej zbiornika u jej podstawy.

Rozwiązanie. Na głębokości h—x_t panuje ciśnienie p_Xl = dg(h — x,), gdzie d oznacza gęstość wody, ag — przyśpieszenie ziemskie. Siła działająca na element ścianki o powierzchni 1 • Ax_i wynosi

P_Xi = p_x. • 1 • Ax_{ = dg (h - x,) Ax_{, moment wywołany tą siłą jest równy

AMx=AP_Xt Xi = dg (hx,-xf) Ax,.

Całkowity moment odginający ściankę wynosi więc

n    n

M= lim Y AM_xi = lim Y dg(hx; — xf) Ax_t =

JM*,-* Oi=l    xi-0 1*1

h    h

= J dg {hx—x²) dx=dg J (hx-x²) dx— o    o

= dg [\hx² - i*³]^fco = dg (i/,³ - ih³) = i dgh³.

Zadanie 20.94. Obliczyć moment bezwładności względem osi Ox obszaru ograniczono lukiem paraboli y² = 2px znajdującym się ponad osią Ox, odcinkiem osi Ox oraz ^dnymi w punktach x = a i x=b, gdzie 0<a<b, przy założeniu, że gęstość powierzchniowa p jest stała.

Rozwiązanie. Moment bezwładności trapezu krzywoliniowego względem osi Ox obliczamy ze wzoru (20.4.3). W danym zadaniu mamy

^Jx = \p I (2px)* dx=\ (2p)ⁱ p | xⁱ dx=\p yflp p ■ § [x⁴]⁵=£p p (b* -a*).

a    a

Zadanie 20.95. Obliczyć moment bezwładności B koła zamachowego o promieniu ^Wnętrznym r i zewnętrznym R, szerokość koła a. Koło zamachowe wykonane jest ¹ Materiału o gęstości y.