195

388 XX. Zastosowania geometryczne całek

388 XX. Zastosowania geometryczne całek

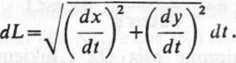
a różniczka luku wzorem (20.2.4)

Jeżeli krzywa dana jest równaniem we współrzędnych biegunowych r=f(o) czym funkcja /(8) ma w przedziale a    ciągłą pochodną i łuk nie ma części wiej

krotnych, to długość luku wyraża się wzorem

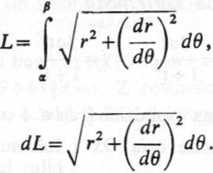
(20.2.5)

a różniczka luku wzorem

(20.2.6)

Uwaga. Gdy    (albo /?-a<2;t oraz r^O), łuk r=f(6) na pewno nie ma części

wielokrotnych.

Zadanie 20.23. Obliczyć długość łuku paraboli y=x² w przedziale 0<x<2.

dy

Rozwiązanie. Stosujemy wzór (20.2.1). Obliczamy pochodną —=2x, a następnie

dx

L= j Jl+4x²dx.

0

Obliczmy całkę nieoznaczoną /= J Vl +4x² dx. Wykonujemy podstawienie 2x=t, skąd po zróżniczkowaniu 2dx=dt, czyli dx=\dt. Mamy więc

/ = i J >/1 +t²dt.

Całkę taką obliczyliśmy w zadaniu 17.43 (str. 337) (przyjmujemy fc = l):

/ = i/V/² + l +iln(t+s/t² + l).

Podstawiając t=2x otrzymujemy

1=\x\! 4x² + \ +iln(2x+v4x² + l).

Obliczamy długość łuku podstawiając granice całkowania:

L = _v/l7+|ln(4 + Vi7)-|lnl, czyli L=Vl7+iln(4+Vl7).

Zadanie 20.24. Obliczyć długość łuku asteroidy x=*acos³1, y=a sin³ t, gdzie a>®' a parametr t przebiega przedział 0<f<2rt (por. zad. 20.3).

Rozwiązanie. Obliczamy pochodne

dx    ,    .    dy ,    . ,

— = — 3a cos²1 sm t,    —— = 3a sin t cos t.

dt    dt

J

Stosujemy wzór (20.2.3); mamy

2it ___    2n _

£,= | V9a²cos⁴isin² t+9a²sin⁴tcos² tdt-ha f Vsin²fcos²t(cos²H-sin²f)</f.

Ale cos

2/+sin²/=l, Vsin² rcos² r = |sinrcost|=^|sin2/|, mamy więc

2*

L = \a J |sin2t|dt. o

Asteroida jest symetryczna zarówno względem osi Ox, jak i względem osi Oy, wystarczy więc przeprowadzić całkowanie w przedziale 0<f^7t; obliczymy wówczas £ łuku (patrz

rys. 20.5). Jest wtedy ¹    ł*

jL=|a Jsin2tdt=|a[-5Cos2t]Jⁿ = |a. o

Ostatecznie L = 6a.

Zadanie 20.25. Obliczyć długość łuku cykloidy x = a (t-sin /), y = a(l-cos t), gdzie a>0, a parametr t zmienia się w przedziale    (por. zad. 20.2).

Rozwiązanie. Obliczamy pochodne

dx    dy

— =a(l-cosr),    —= a sini

dt    dt

i stosujemy wzór (20.2.3); mamy

2n__2it    _

L= J Va²(l—cost)²+a²sin² tdt = a J v(l — cosf)² + sin²idt = o    o

2* ______ 2n -

= a | VI—2cost+cos² r+sin² tdt = a J V2(l — cos t)dt.

o    o

Stosujemy teraz wzór trygonometryczny 1 -cos t=2 sin² \t i otrzymujemy

2k

L = 2a | |sin -1| dt. o

Ale w granicach całkowania, tj. dla 0^t^2n, jest sin-^/^O, mamy więc

2it

L = 2a J sin \ tdt = 2a [ — 2 cos jt]o’^t = 8a. o

Długość łuku cykloidy jest więc równa poczwórnej średnicy toczącego się okręgu ⁽Patrz rys. 20.4).

Zadanie 20.26. Obliczyć długość łuku spirali logarytmicznej r = ae^ke, gdzie a>0. a parametr 0 zmienia się w przedziale O<0<a (por. zad. 20.4).

Rozwiązanie. Stosujemy wzór (20.2.5); mamy

r = ae‘®, skąd ^-=ake^k\ dO