196

390 XX. Zastosowania geometryczne całek

Więc

390 XX. Zastosowania geometryczne całek

i ostatecznie

L = a]y./e^2ke + k²e^ned0 = a ) V(1 + k²)e^2kedd = o    o

= a Vl+fc² J e^kedd = a Vf+F^

\l+k²

L = a

-(* -1).

e^kx-l

Uwaga. Przyjmujemy a>0. Jeżeli k<0, to 1 <0, ale ponieważ —-—>0, przeto

I>0.

Zadania

Obliczyć długości następujących łuków (zad. 20.27 - 20.62):

y²=4x³, y>0, OsSJtsgf, 9y² = 2x³, 0<jc<2.

9y² = jc\ 0<x^l2. 2y²-x³=0, 0śxś2. y² = 2x-x², 0^x^l.

20.27.

20.29.

20.31.

20.33.

20.35.

20.37.

20.39.

20.40.

20.41.

20.42.

20.43.

20.44.

20.45.

20.28. 9y²=4x³, 0^x^3.

20.30. 3y²=4x³, O^jc^I.

20.32. 2y² —3jt³=0, 0«x<2. 20.34. y = 2jx, A(1,2), B(9,6). 20.36. 2y²=x — 2x²,

y = 2yjx, 0<jr<l.    20.38. y=2 J3x, 0<x<l.

Łuk paraboli półsześciennej (paraboli Neila) y=\{x— 1)* w przedziale 1

Łuk krzywej y = ln sin x w przedziale

Łuk krzywej y=l —ln cos x w przedziale 0^x^Ąn.

X

Łuk linii łańcuchowej y = acosh—, a>0, w przedziale —

a

Łuk krzywej logarytmicznej y~\nx w przedziale _N/3^x^2_N/2.

Łuk krzywej = ln (1 —^c²) w przedziale

Łuk krzywej y = - ln tgh \x w przedziale l<x^2.

20.46. y = arcsin;r+\/l— x², —l^x^l. 20.47. y² — ^

20.48. x = iy²-ilny, l<y<2.    20.49. y^e\ zf(0, 1), B{\, e).

20.50.    Łuk kardioidy r = a(l+cos0), a>0, w przedziale 0^#<7t.

20.51.    Łuk spirali Archimedesa r = ad, a>0, w przedziale O<0<1.

20.52.    Łuk spirali hiperbolicznej r = a/d, a>0, w przedziale

20.53.    r=2a cos 0 (okrąg).

20.54. r~----, —

1 +cos ę

20.55.    Łuk krzywej x = t², y = t — ^t³ w przedziale 0</<,/3.

20.56.    Łuk rozwijającej okręgu x = r(cos t + t sin t), y=r(sin t-t cos /), r>0, w przedziale

20.57- Łuk krzywej x — 2t cos t+(t² — 2) sin t, y=2t sin t—(t² — 2) cos t, w przedziale

20.58. Łuk krzywej x = a cos⁵ ~t, y=a sin⁵ ~t, a>0, w przedziale 0</<7t.

20.59.    Łuk cisoidy Dioklesa x=2asin²t, y = 2as'm¹ t tg t,    .

20.60.    Łuk kardioidy x = 5 cos t (1 +cos t), y = 5 sin t (1 +cos t) w przedziale 0<rs$2rt.

20.61.    x=a cos⁴ /, y=u sin⁴ r, a>0, w przedziale 0<r<^-7t.

20.62.    x=ęcos⁵ /,j> = asin⁵ t, a> 0, w przedziale 0<x<o.

§ 20.3. OBLICZANIE OBJĘTOŚCI I POLA POWIERZCHNI BRYŁ OBROTOWYCH

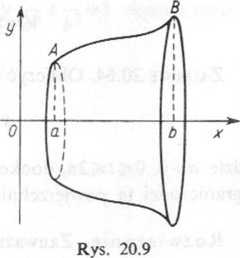
Niech dany będzie luk AB (rys. 20.9) krzywej o równaniu y=f(x), gdzie /(x) jest funkcją ciągłą i nieujemną w przedziale (a, b). Wówczas objętość bryły obrotowej ograniczonej powierzchnią, która powstaje, gdy łuk AB wraz z rzędnymi w końcach łuku obraca się dookoła osi Ox, obliczamy według wzoru

i>

(20.3.1)    V = n$y²dx.

Pole powierzchni obrotowej powstałej przez obrót łuku śB dookoła osi Ox obliczamy według wzoru

B    b _

(20.3.2) S

■²”I

ydL-2n

J\/l +

dy

dx

dx,

Ptzy założeniu dodatkowym, że funkcją y=f(x) ma w przepale a^.x^b ciągłą pochodną.

Jeżeli równanie łuku AB dane jest w postaci parametrycznej x=g(t), y = h{t), /,

P^fzy czym obie funkcje mają w tym przedziale ciągłe pochodne, funkcja g(t) jest w tym Przedziale stale rosnąca albo stale malejąca, a funkcja h(t) przybiera wartości nieujemne, ^,f> na objętość bryły obrotowej mamy wzór

⁽²⁰-3.3)    _{V = n}

^na pole powierzchni obrotowej wzór

'20.3.4)

(1