207

412 XX. Zastosowania geometryczne całek

Gazy wieloatomowe wykazują zależność ciepła właściwego od temperatury według równ_a nia c=c₀ + at + bl². Obliczyć ilość ciepła potrzebną do ogrzania danej masy gazu ni ₀₍j' temperatury t, =0 do t₂ = z.

Rozwiązanie. Mamy

at^1		( at^2 br^3'
fS	3 h '	r ^+ 2 ^+t

Zadanie 20.153. Wskutek działania ciśnienia p następuje zmiana objętości gazu

od

V2

v_t do v₂. Praca wykonana przez ten gaz, wyraża się wzorem L= \p dv. Wyznaczyć pracę przy przemianie izobarycznej, tzn. przy p = const.

Rozwiązanie. Mamy

Vl    V2

L= j pdv = p J dv=p(v₂-v₁).

U|    Vl

V2

Zadanie 20.154. Obliczyć pracę L = J pdv wykonaną przez rozprężający się gaz. Objętość

Ł‘l

początkowa gazu wynosiła u, =2500 cm³, końcowa zaś y₂ = 7500 cm³, ciśnienie początkowe Pi = 5 kG/cra², rozprężanie odbywało się przy stałej temperaturze (pu=const).

Rozwiązanie. Wyznaczamy funkcję określającą objętość v w zależności od ciśnieniap: mamy

12500

pv=p_t v₂ = 2500-5 = 12500 . skąd p=--

v

Szukana praca wynosi więc

*>2

L

7500

= j* pdv= 12 500 | — =

12 500 ln y|25oo =

ui    2500

= 125001n    125001n3kGcm = 1251n3kGm .

V2

Zadanie 20.155. Obliczyć pracę L= J pdv wykonaną przez rozprężający się adiabatycznie gaz, jeżeli objętość początkowa wynosiła u,, końcowa zaś v₂, a ciśnienie początkowe wynosiło p₂. Równanie adiabaty ma postać pv^k=p_lv\, gdzie &=const.

.    .    Pi^vi

Rozwiązanie. Z równania adiabaty wyznaczamy ciśnienie p — —r— , a więc

v

praca wynosi

V2    VI

szukana

. r , _k r dv * r® T*

L= I pdv=PttĄ J -jj_jr = p₁»i I—-J =P<v₂-

1-k l—k    k 1 -k

»2    -»I Pl V_l~PiV\V₂

1 -k

k-1

podstawiając p_iv\=p₂v^k2 otrzymujemy ostatecznie

_L_Pl Vj~P2 v₂ k-1

Zadanie 20.156. Obliczyć siłę nacisku wody na pionową ścianę w kształcie trójkąta (rys. 20.18). Powierzchnia wody w zbiorniku sięga podstawy trójkąta a, tzn. że jej poziom jest równy wysokości trójkąta h (przyjąć ciężar właściwy wody d=l G/cm³).

a

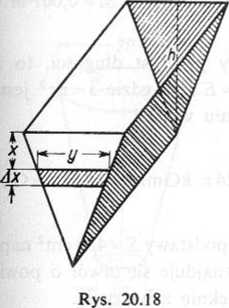
Rozwiązanie. Siłę nacisku obliczamy jako całkę z ciśnienia p względem ds (pcwierzchni).

(0    F= | pds ,

o

gdzie ds=y dx, p=6x, a x, y jak na rysunku 20.18. Wyznaczamy związek między x a y; mamy

h—x y    h—x

——, skąd y = _a-——. ha    h

^stawiając wyznaczoną wartość na y i p — óx oraz 'ds=ydx do całki (1) otrzymujemy

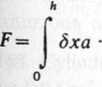
h-x ~

h

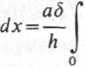
(hx-x²)dx=

aó

~h

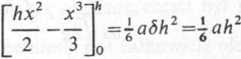
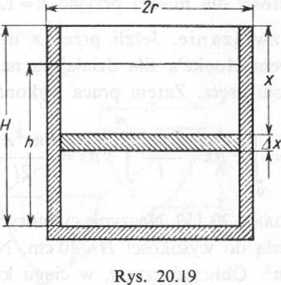
Zadanie 20.157. Obliczyć pracę, jaką trzeba wykonać, ażeby wypompować wodę ^Cylindrycznego basenu (rys. 20.19). Promień podstawy basenu wynosi r = 0,5 m, głębokość *3(11, poziom wody liczony od dna h — 2,8 m (przyjąć ciężar właściwy wody <5= 1000

*tym³).