192

382 XX. Zastosowania geometryczne całek

Zadanie 20.1. Obliczyć pole obszaru ograniczonego linią

(1)    x=acost, y=b sin t,

gdzie a>0, b>0, a parametr t przebiega przedział 0</<2ir.

Rozwiązanie. Z układu równań (1) mamy

x    y

— = cos t,    — = sin t.

a    b

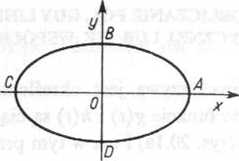
Rys. 20.3

Podnosząc te równości do kwadratu i dodając stronami otrzymujemy

(7)⁺(i) ■^c°^s2,+sin2'¹ “^yii .

Szukamy więc pola ograniczonego elipsą (rys. 20.3).

Funkcja x = a cos t w przedziale    jest malejąca, a więc pole ograniczone lukiem

ABC i odcinkiem CA obliczamy według wzoru (20.1.2). Zauważmy, że w przedziale 0</<ji funkcja y=b sin t jest nieujemna. Mamy więc

n    n

?! = — J bsin f ( — dsin t)dt = ab J sin²1 dt. o    o

Natomiast w przedziale 7t<r<27t funkcja x = a cos t jest rosnąca, a więc pole ograniczone łukiem CDA i odcinkiem CA obliczymy według wzoru (20.1.1). Ale w przedziale mamy równość |sin r|= — sin t, a więc wzór (20.1.1) daje

2n    2n

P₂= j |bsini|( — asint)dt = ab Jsin²/ dt.

1t    1t

Sumę pól można wyrazić jedną całką

2n

P = P_y + P₂ = ab | sin² tdt. o

Biorąc z zadania 18.3 (str. 350) całkę j sin² t dt = %t — i sin 2/ otrzymujemy

P = ab[jt-± sin2/]o’'=/tub.

g^DANiE 20.2. Obliczyć pole ograniczone odcinkiem osi Ox i lukiem cykloidy jyeślonej równaniami parametrycznymi (por. zad. 7.20):

x=r(t—sint),    y = r(l—cost).

,dzie r>0, a parametr t przebiega przedział 0</<2tt (rys. 20.4).

Rozwiązanie. Badamy, czy równania cykloidy spełniają warunki podanego twier-

dx

dzenia. W tym celu obliczamy pochodną —=r(l —cos /). Biorąc pod uwagę, że 1 —cos f ^ 0, dx    ^dt

stwierdzamy, że —>0, a więc funkcja x—r(t- sin r) jest rosnąca. Do obliczania pola dt

obszaru stosujemy więc wzór (20.1.1); mamy

2n    2 n

P= J |r(l-cos0|r(l-cosf)rft = r² j(1 -cost)²dt. o    o

Obliczamy całkę nieoznaczoną

J (1—cos t)²dt=^t — 2sint+jsin2t.

Obliczamy poszukiwane pole

P = r² [f t - 2 sin t + \ sin 2t]l* = 3nr².

Pole ograniczone lukiem cykloidy oraz osią Ox równa się potrojonemu polu toczącego ^Sl? koła.

Zadanie 20.3. Obliczyć pole ograniczone asteroidą określoną równaniami parametry-^cznmi (por. zad. 7.21 i 20.22):

x = acos³t,    y = asin³r,

^^z‘^{e Q}>0, a parametr t przebiega przedział 0<f<27t (rys. 20.5).

. Rozwiązanie. Rozważania takie, jak w zadaniu 20.1 doprowadzają do wniosku, ^ZePole P₁ w przedziale O^t^n należy obliczyć według wzoru (20.1.2), a pole P₂ w prze-według wzoru (20.1.1); ostatecznie otrzymamy pole asteroidy P=P_l+P₂-Można jednak wyzyskać symetrię asteroidy (rys. 20.5):