002 (64)

Zestaw 3

Zadanie 1. (3 pkt)

Oblicz pole figury ograniczonej wykresami funkcji f(x) = |a: + 4| — |x| i g(x) = |2x|. Zadanie 2. (5 pkt)

Wyznacz wartości parametru /c, dla których dziedziną funkcji f(x) = y/(l - k²)x² + (k - 1)* + 1 jest zbiór liczb rzeczywistych.

Zadanie 3. (7 pkt)

Ramiona trapezu opisanego na okręgu mają długości 13 cm i 15 cm, pole trapezu jest równe 168 cm², a kąty przy jego dłuższej podstawie są ostre. Oblicz pole trójkąta, którego wierzchołkami są końce dłuższej podstawy trapezu i punkt przecięcia jego przekątnych.

Zadanie 4. (5 pkt)

Punkty A i B są punktami przecięcia okręgu (x — 2)² + (y + l)² = 25 z prostą y — -2x + 8, a odcinek AC jest średnicą tego okręgu. Oblicz pole trójkąta ABC, jeśli punkt A ma obie współrzędne dodatnie.

Zadanie 5. (4 pkt)

Dany jest ciąg o wzorze ogólnym

1 + 3 + 5 + ... + (2n + 1)

a_n = -—ó--ⁿ-

n ~t Z

a)    Oblicz dziewięćdziesiąty ósmy wyraz ciągu (a_n).

b)    Zbadaj monotoniczność ciągu (a_n).

Zadanie 6. (5 pkt)

Promień podstawy stożka jest równy 3, a cosinus kąta nachylenia jego tworzącej do płaszczyzny podstawy wynosi Oblicz długość krawędzi sześcianu wpisanego w ten stożek (sześcian jest wpisany w stożek, jeśli cztery jego wierzchołki należą do podstawy stożka, a pozostałe cztery do powierzchni bocznej stożka).

Zadanie 7. (4 pkt)

Wyznacz dziedzinę i miejsca zerowe funkcji f(x) = log(.T² + x) — log(3.x + 24). Zadanie 8. (4 pkt)

Prosta k przecina proste y — 2x = 0it/ + x — 3 = 0w takich punktach A i B, że punkt 5(4,2) jest środkiem odcinka AB. Podaj współrzędne punktów A i B oraz wyznacz równanie prostej k.

Zadanie 9. (4 pkt)

Dane są dwa trójkąty prostokątne. Długości boków każdego z nich tworzą ciągi arytmetyczne. Wykaż, że te trójkąty są podobne.

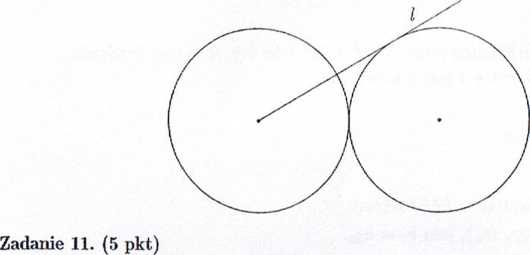
Zadanie 10. (4 pkt)

Dane są dwa styczne okręgi, każdy o promieniu LO. Ze środka jednego z nich poprowadzono pólprostą l styczną do drugiego okręgu (rysunek poniżej). Oblicz pole obszaru ograniczonego tymi okręgami i półprostą l.

Z urny, w której znajdują się kule o numerach: 1,2,..., n (n > 2), losujemy kolejno bez zwracania dwie kule. Numery wylosowanych kul tworzą parę (x, y). Dla jakich wartości n prawdopodobieństwo tego, że para (x, y) spełnia warunek \x — y| = 2, jest mniejsze od 0,25?

13. Zestawy maturalne 81