205 2

408 XX. Zastosowania geometryczne całek

Całkę nieoznaczoną obliczamy całkując przez części:

J e^_3,sin-j7trc/f= —je“³'sinijtt +|a J e^_3'cos§ntdt =

= -ie“³'sinijct-₁k7te^_3'cos    J e“³'sini7ttdf ;

otrzymujemy

36 + -²

3 4“ r

——    e^-3,sinż-7tf(/t=—Je^-3'sin-jUt-j^Tte^-3'cos Jnf + C ,

skąd

Je ³¹ sin—

12

36+ti

_że ^3tsin-jTtf — - *—₂ e~^3tcos;7tt + C₁ , 36+ji

a więc

r ¹²    -s. • .    ²*    -3. .    T

c/=--= e sm-^Tif——-= e cos^tc t =

L    36+ti^2    2    36+ti^2    2    Jo

12    .    2ix    12    ₀ .    2n .

--_Te sinjt —--_;e cosn +-^e sin0 +-= e cos0=

36+7t²    36+ti²    36 + ti²    36+ti²

2ti

e~⁶ +

36+ti² 271    271

36+7t²    36+7i² 36+ti²

(e +1) •

Zadanie 20.146. Wyznaczyć napięcie U pomiędzy punktami + i B pola elektrycznego wytworzonego między okładkami kondensatora walcowego o długości / (rys. 20.16). Od

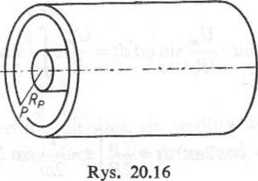
ległość punktu A od osi symetrii wynosi R_A, punktu zaś B jest R_B. Natężenie pola elektrycznego w dowolnym punkcie P pola, odległym o R_P od osi symetrii kondensatora, wyraża

się wzorem K =    ■ , gdzie Q - ładunek elektryczny zgromadzony w kondensatorze.

2nsRl

e — stała dielektryczna.

Rozwiązanie. Mamy

Rb

Rb

O Rb

(In R_B—\nR_A) =    - ln

2nel R_a

f    Q CdR Q

U= KdR — ^—    ~ = ~

J    2nsl J R 271 el

Ra    Ra

Zadanie 20.147. Naładowany elektrycznością kondensator jest rozładowany przez _wj_en opór czynny tak, że natężenie prądu w obwodzie przedstawia wzór i=5e~'ⁿ°. W    ’²

Obliczyć, jaka ilość elektryczności q= J idt przepływa przez obwód w czasie 0</<10.

Rozwiązanie. Mamy 10 10

ą= | idt = 5 J e"'^/1O^=-50[e"'^/lo]i°=-50(e"¹-l) = 50^.

o    o

Zadanie 20.148. Obliczyć, o ile wydłuży się pręt o kształcie podanym na rysunku 20.17 pod wpływem obciążenia siłą P.

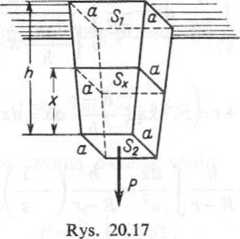
Rozwiązanie. Wiemy, że zgodnie z prawem Hooke’a przyrost długości

h

(1)    Jx- J dx,

O

gdzie h długość pręta, S_x przekrój poprzeczny pręta w odległości x od początku pręta, ^a E moduł Younga. Oznaczmy przez 5i pole górnej podstawy, a przez S₂ pole dolnej podstawy; wówczas

h    x

Szukany przyrost długości wynosi

h    h

dx

S_t — S₂ S_x — S₂    S_l — S₂

skąd    S_x =— -x + S₂ .

^ph f

J ES, ejs.-s, £<S,-S,)J

o    o —: x + o₂    o

dx

o x +

Ph r I hs₂ T Ph /

=- ln \x4---—--(ln

£(Si-S₂) L | S_x—S₂ Jo E(S_l—S₂) \

s,-s₂

hS₂

h +

Si-S;

-ln

hS₂

Si-S_:

i ^S*

ln ——

Ph

E(S_x-S₂) s