Scan10038

2. Obszar D a R~ nazywamy obszarem normalnym względem osi OY. jeżeli jest określony nierównościami;

D_or-

c<y<d

<Pi(y) ę₂iy)

PRZYKŁAD

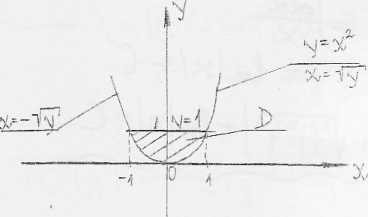
Obszar D ograniczony linia osi 0X jak i OY, ponieważ:

x²<y<lr

0<y<\

DEF«

Obszar D d R~ nazywamy regularnym, jeżeli jest on sumą obszarów normalnych (względem osi 0X lub osi OY), które nie mają wspólnych punktów wewnętrznych.

PRZYKŁAD

Obszar D d R² ograniczony liniami :y = 2x² i >>=|a:|+1 jest obszarem regularnym złożonymi z dwóch obszarów normalnych względem osi 0X|

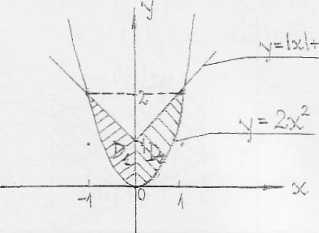
-1 < x < 0 i2x² <y<-x+lf f 0<x<l ² \2x²<y<x+l