015

Zad. 14. Obliczyć moment bezwładności względem osi Oy obszarów ograniczonych krzywymi:    a) y = co$x, 0 < x < |7r, y — 0, x = 0, b) y = 0, y = 1 - z, y = 1 + x,

c) y = (x + 4)_v^/-x₁ x = 0, d) £/ — ^ arctg a:, x — 0, x — 1, e) i/= y^r, x = 1, £ = 9, y^l).

Zad. 15. Obliczyć Środek ciężkości obszarów ograniczonych następującymi krzywymi:

a) y = sin# (dla 0 < x <ir), y — 0, b) y = e²*, y = 0, x - 0. x - 1, c) y = ydr, £/ =

0, x = 1, d) 0 < jy < n/25 - x², e) «/ = 4 - x², ?/ = 0, f) yćr H- \/y = 3, x = 0. y = 0, g) y = lnx, y = 0, x = e, h) y = 1 + cosx (dla -n < x < tt), y = 0, i) y = x - -1, x = 1, j) x² + y² = 4_f x > 0, y > 0.

Zad. 16. Obliczyć w przybliżeniu drogę przebytą przez samochód, którego prędkość w chwili i wynosiła f(t) km/godz jak na załączonych wykresach

a)    b)    c)

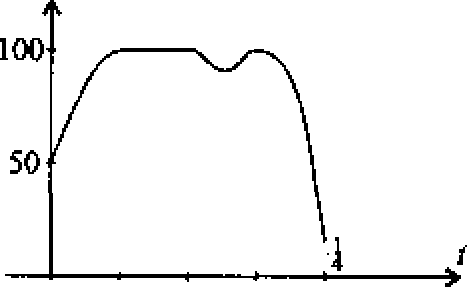
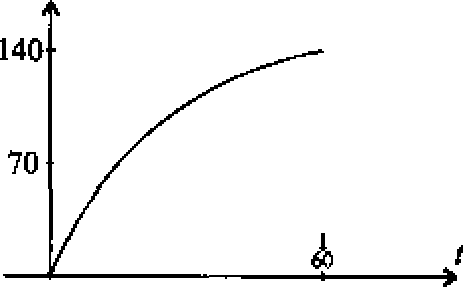
Zad. 17. Obliczyć drogę przebytą przez kulę toczącą się po pochyłym torze:

a)    w ciągu pierwszych 5 sekund od startu, jeżeli wiadomo, że jej prędkość w chwili t wynosiła At cm/sek.

b)    od upłynięcia drugiej sekundy do upłynięcia szóstej sekundy, jeżeli wiadomo, że jej prędkość w chwili t wynosiła 3£ cm/sek,

c)    w ciągu pierwszych 7 sekund od startu, jeżeli jej prędkość w chwili i wynosiła \/4 4- 3£ — 2 m/sek.

Zad. 18. Prędkość samolotu na pasie startowym w ciągu początkowych 10 sekund po

starcie wynosi 21 + 2 v^100 t m/sek. Jaką odległość przebędzie w tym czasie samolot? Zaraz po upływie dziesiątej sekundy samolot zaczyna się wznosić i przez kolejną minutę

ma prędkość 20 + 2 v^100£ m/sek- Jaką odległość przeleci w ciągu tej minuty?

Zad. 19. Prędkość pewnej rakiety w czasie początkowych 8 sekund po starcie wynosi liffi m/sek, przez następne 12 sekund wynosi 2£ + 40 m/sek w chwili £, a przez kolejne 10 sekund jest stała. Obliczyć drogę pokonaną przez rakietę: a) przez początkowych 8 sekund, b) przez początkowych 20 sekund, c) przez początkowych 30 sekund, d) od upływu 15“Oj do upływu 25-ej sekundy

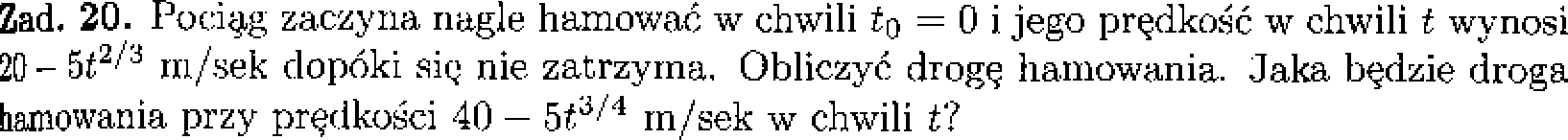
Zad. 21. Obliczyć pracę potrzebną do wypompowania cieczy o podanym ciężarze właściwym z opisanego zbiornika na podaną wysokość od dna zbiornika:

a) zbiornik w kształcie prostopadłościanu o podstawie 8 na 5 metrów i wysokości 1,5 metra całkowicie wypełniony wodą ma być wypompowany przez swój wierzch (czyli na wysokość 1,5 metra od dna zbiornika),

99