32991 ScanImage05

Przy założeniu, że wymiary materiału stykowego tworzącego zestyk są w

wówczas symetryczne względem osi prostopadłej do powierzchni S_p1

stosunku do wartości S_p1 znaczne, możemy przepływ prądu przez powstałe przewężenie rozpatrywać jako przepływ z jednej półprzestrzeni nieograniczonej o oporności właściwej p do drugiej półprzestrzeni również nieograniczonej o takiej samej oporności właściwej, poprzez powierzchnię przejścia S_p1 . Otrzymamy

trójwymiarowe pole przepływowe. Rozpatrując każdą półprzestrzeń oddzielnie możemy obliczyć oporność dla przepływu prądu przez powierzchnię S_p1 do nieograniczonej półprzestrzeni materiału o określonej oporności właściwej w sposób taki, jak obliczamy oporność uziemiacza powierzchniowego. Zauważmy jednak, że powierzchnie ekwipotencjalne i izotermiczne tego pola będą elipsoidalne, wobec czego linie pola przepływowego w przekroju rysunku będą hiperbolami. Obliczenie oporności byłoby utrudnione. Możemy jednakże takie pole przepływowe zastąpić równoważnym polem, w którym elektrodę płaską zastąpimy równoważną elektrodą półkulistą rys. 2 . Wówczas pole potencjalne i przepływowe będzie znacznie prostsze, bowiem powierzchnie ekwipotencjalne będą powierzchniami kulistymi, a linie pola przepływowego w przekroju rysunku liniami prostymi. W tym przypadku zastępcza elektroda półkulistą posiadałaby promień

?

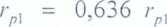
gdzie:

r₀ - promień elektrody zastępczej półkulistej.

Oporność przejścia R₀ dla przepływu prądu z elektrody półkulistej o promieniu r₀ do półprzestrzeni nieograniczonej o oporności właściwej p wynosi:

R,

P

Wobec tego dla elektrody płaskiej o promieniu r_p1 oporność wynosi:

R,

p 71

P

2 7i ■ 2 r,

4 r

Oporność przejścia zestyku składa się z dwóch oporności szeregowo połączonych i wynosi:

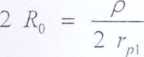
R

gdzie:

oporność przejścia zestyku jednopunktowego. Wykorzystując równanie [3] otrzymujemy ostatecznie:

5