Matematyka 2 A9

418 VI Elementy stutysh ki mairmaiu znef

^I-X|,    |i₂~^(2X,-rX,).    A,-|(2X, + X₂-X,j_f

M,=i(X,+X₂).    m₅=|(X, +X₂ + Xj)

wybierzemy: a) estymatory nicobeiążone parametru p. b) najefektywniejszy estymator spośród nieobciążonych.

a) E(|i,) = p.    fc(m₂ ) = -i<2HX| + EX_:) = -^(2p + p) = p .

=    E(ji₄)=p_f E(p<)=p

Zatem tylko (i3 jest estymatorem obciążonym.

b)    Var(p, )= VarX, = VarX = a".

Var( p ₃) = ^( 4 VarX, + VarX ₂) - |a^:,

Var(p.,)=-^(o* *a^:)=-^v^:,    Var(p₅)= VarX₃ = |o¹.

W danym zbiorze estymatorów najefektywniejszym jest więc estymator p₅ = X$. czyli średnia arytmetyczna próby (X. .X_:,X,)    ■

3. Od estymatora wymaga się aby oszacowanie (4 I) było tym

lepsze, im liczność próby jest w iększa W znacznym stopniu warunek ten

spełnia estymator zgodny. Mówimy, zc estymator 0_n parametru 9 jest

/godny, gdy dla każdego f.>0

(4.5)    Hm P(|0_B -0|<e)* I.

u -»«

Zatem estymator Zgodny dla dużych liezności próby, tj dla dużych n. przyjmuje z pr-stwem bliskim jedności wartości bliskie estymowanemu parametrowi.

PRZYKŁAD 4.2. Ze słabego prawa wielkich liczb Berno-ulliego (por. tw 2.2) wynika, że częstość wzglądem S„/n zdarzenia A w serii n doświadczeń Bemoulliego |cst zgodnym estymatorem parametru p, tj pr-stwa sukcesu A w pojedynczym doświadczeniu. p=P(A).    ■

ESTYMATORY WARTOŚCI OCZEKIWANEJ Najczęściej stosowanym estymatorem p nieznanej wartości oczekiwanej p = EX

cechy X jest średnia arytmetyczna X„ PLP (X,,X_:.....X„). p=X_n,

określona wzorem:

O jej zaletach or/eku następujące

TWIERDZENIE 4.1.    1) Średnia arytmetyczna X_n PI.P

(X,.X_:_____X_n) cechy X o dowolnym rozkładzie jest nicob-

ciązonym i zgodnym estymatorem nieznanej wartości oczekiwanej p (jeśli ta wartość oczekiwana istnieje);

t4.5) EX„ = p oraz limP(|X„-p|<e)=l przy dowolnym e>0.

2) Gdy cecha X ma rozkład normalny N(p.a), to średnia arytmetyczna jest równie/' najefektywniejszym estymatorem wartości oczekiwanej p

Dowod. Równości (4.5) wynikają bezpośrednio 7 twierdzeń 1.1 i 2.1, jeśli uwzględni się definicję PLI*. Dowod tezy 2) pomijamy.

Innym, stosownym estymatorem wartości oczekiwanej jest średnia arytmetyczna wartości skrajnych

(4.6)

gdzie X_min

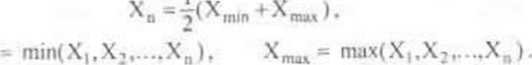
ESTYMATORN WARIANCJI Najczęściej stosowanymi estymatorami nieznanej wariancji ar = VarX cechy X są:

t) wariancja S^: PLP (X,.X₂,.._MX_(I) określona wzorem ¹

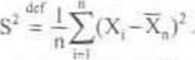
3) wariancja S„ PLP (X,,X₂.....X_n ) określona wzorem

1

skorygowana wariancja Sf PLP (X,.X₂.....X_n) określona

wzorem:

(4.8)