Matematyka 2 D1

440 V1 Elementy sum sn ki matematycznej

440 V1 Elementy sum sn ki matematycznej

(d)

W = A|uA₂u-vA_kl A,nAj=0, gdy i*j.

Niech dla i = 1,2,...,k. p, oznacza pr-stwo [liczone według rozkładu zadanego hipotezą ll₀) tego. że cecha X przyjmie wartość z i-tej klasy w próbie jednoelementnwej:

p, = P(XeA,|II₍₎);

zatem stosownie do postaci (a), (b), (c) hipotezy H_u

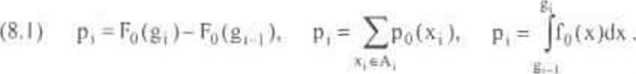
Niech, dla i = 1.2,...,k, N,oznacza ZLS. której wartościami są liczności n, i-tej klasy wc wszystkich rt-elementowych próbkach (x,.....x_n )danych w postaci szeregu rozdzielczego o klasach postaci (d).

Pr/y tych oznaczeniach omawiany test jest ciągiem następujących czynności.

I) Statystyką testową jest statystyka    (czytamy: chi kwadrat)

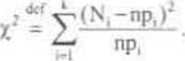
Ula danej próbki obliczamy jej wartość yj„_ip:

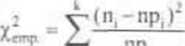
Zauważmy, źc w różnicy n,-np₍ odjemna n, - to liczba elementów próbki n-elemcntowej, które znalazły się w i-tej klasie, natomiast odjemmk np₍ - to liczba elementów w n-elementowej próbce, które powinny sic znaleźć w i-tej klasie, gdyby cecha X miała rozkład pr-stwa zadany hipotezą H₀ (gdyż w iloczynie np. czynnik p jest obliczony według rozkładu pr-stwa zadanego hipotezą H„ i wobec tego iloczyn np, może być traktowany jako wartość oczekiwana liczby sukcesów w schemacie n prób Rernoulliego z pr-stwem p, sukcesu w pojedynczej próbie, sukcesem jest tu przyjęcie przez ZL X wartości 7 i-tej klasy). Zatem różnica n,-np, mierzy "niezgodność" w i-tej klasie liczności empiry cznej n, z licznoicią hipotetyczną np,.

2)    Dowodzi się, że przy założeniu prawdziwości hipotezy H₀ dystrybuanta statystyki (8.2) przy n->oc jest zbieżna do dystrybuanty ZL o rozkładzie chi-kwadrat z k-l-m stopniami swobody, gdzie m jest liczbą nieznanych parametrów rozkładu zadanego hipotezą H₀ i szacowanych tzw. metodą największej wiarogodności na podstawie danej próbki cechy X.

3)    Z tablic rozkładu chi-kwadrat odczytujemy kwantyl xl i-m.i-a» gdzie u oznacza poziom istotności. Budujemy zbiór krytyczny K_a®<Xk-,-m.H.i^+gc)* Bierzemy tu prawostronny zbiór krytyczny, ponieważ duże wartości y]_mp świadczą przeciwko hipotezie H₀. Hipotezę H₀

odrzucamy na poziomie istotności a, gdy xlm _P. eK_a Jeśli xL_P 10 orzekamy: dana próbka nie przeczy hipotezie H₀.

U w a g i . 1) Rozkład chi-kwadrat statystyki (8.2) jest rozkładem granicznym, dlatego omówiony tu test stosujemy, gdy próbka jest duża (n>50).

2)    Liczności n, nic mogą być zbyt małe (n,>6). Ten warunek narzuca konieczność łączenia sąsiednich klas, gdy n_; <6.

3)    Test chi kwadrat ma zastosowanie zarówno do cechy ciągłej jak i skokowej.

PRZYKŁAD 8.1. Dostawca towaru twierdzi, że liczba sztuk niezgodnych z normą nic przekracza 6%. W I OO-elementowcj próbce z całej dostawy stwierdzono 9 sztuk niezgodnych z normą. Czy ta liczba przeczy zapewnieniom dostawy? Przy szukaniu odpowiedzi przyjmujemy poziom istotności a=0.05.

Niech X oznacza ZLS przyjmującą wartość l, gdy sztuka w próbce odpowiada wymaganiom normy i 0 w przypadku przeciwnym. Zapewnienia dostawcy traktujemy jako hipotezę zerową łl₀, czyli:

0

0,94

p, 0,6

H₀: ZL X ma funkcję pr-stwa postaci:

Zastosujemy test chi kwadrat 1) Obliczamy

_:    ^(n,-np,)^:_(9-l00 0,06)^: (91-100 0,94)²    ₆

Ł np,    100 0,06    100 0,94