MATEMATYKA038

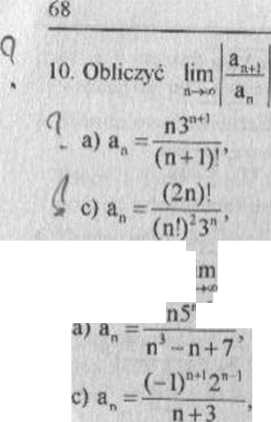
0. Ciągi i szeregi liczbowe

. gdy:

⁷.b)a„=(-ir^.

£

s d)a„=(-D

II. Obliczyć lims/faj, gdy:

n5^r

b) a_n=M)

d) a =

n^f

in. i (n + 2)!

n5

n*l

_n 2n‘ - n + 3

3n² +2

.ml

5n^: +2n-3

Odpowiedzi.

4    a) Rosnący, b) malejący, c) malejący, d) niema lej ącv.

15?' bT™’^nia,CJąC>’ ‘ ^b)'^d)’ °^^unicwłn-^v - ^a>- b)» d); georactiyczny - a), b), c),

⁷ «) a², b) 1, c)-, d)0.

3

5    a)2.    b)+«,    c)0,    d)i, c)i, l)~_t g)-^, h) i)    I.

j)3,    k)+oo,    1)0,    ł)0, m)-H3c, n)I, o) —1, p)-oo,    r) j,

s)0.    l)0, u)(), v)e ^J, w) e⁸, x)granica nie istnieje, v)    I. z)0.

'    ^u)°»    ^b) .    c)    . d) I, e)-oo. g)-oo,    h)-oo.

i) +00, j) +30, k) -łoo ,    1)0, I) it/2, m) +00, n) Jł/2,    0)0,

P)0. r) 0.6, s) 2, 1)1. u) 8 I0.*)0, b)c, c) 4/3, d) +ao,

U n)3, b) 1. c)2, d) +».

2. Szeregi liczbowe

69

2. SZEREGI LICZBOWE.

SZEREGI LICZBOWE. Niech będzie dany skończony ciąg liczbowy a,, a?,..., a_k. Wyrażenie

k

a₁ + a_J+...+a_k-2>"

n»l

jest sumą skończonej liczby składników i nazywa się je krótko sumą.

Niech będzie dany nieskończony ciąg liczbowy (a_n). Wyrażenie

•9

a,+a₂+a,+—, czyli £a_n

!*■» I

nazywamy nieskończonym szeregiem liczbowym (krótko: szeregiem), przy^r czym a_n nazywamy n-tym wyrazem tego szeregu.

Ciąg (S_n) określony następująco.

S_n-a₁+a₂+a₃-h--+a_n, neN,

nazywamy ciągiem sum częściowych szeregu £a_n.

n=l

Szereg ]Ta_n nazywamy zbieżnym, gdy jego ciąg sum częściowych (S_n) jest zbieżny, przy czym granicę

S = lim S.

nazywamy sumą tego szeregu i zapisujemy wtedy

CD

X^a„=s.

i»*l

Szereg £a_n nazywamy rozbieżnym, gdy jego ciąg sum częścio-

n»l

wych jest rozbieżny.

CD

Jeżeli szereg £a„ jest rozbieżny i jego ciąg sum częściowych ma

n«l

granicę niewłaściwą, tzn limS =±oo, to mówimy, żc szereg jest roz-

n-»®