MATEMATYKA041

74 II. Ciągi i szeregi liczbowe

Ponieważ twierdzenia proste i przeciwstawne są równoważne, więc prawdziwe jest również twierdzenie przeciwstawne do twierdzenia 2.4.

TWIERDZENIE 2.4' Jeżeli lim a_n * 0 albo lim a„ nic istnieje,

to szereg £a_n jest rozbieżny.

Na przykład szeregi

y s—t , y n sin i, y cos n, ** 2n +■ I    n

są rozbieżne, gdyż

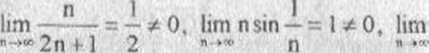
= — * 0, lim n sin — = l * 0, lim cos n nic istnieje.

Twierdzenie odwrotne do twierdzenia 2.4 jest fałszywe, czyli zbieżność Jo zera ciągu (a.,) nie jest warunkiem wystarczającym zbieżności szeregu Va

Istotnie, ciąg (1/n) ma granicę równą 0, a szereg £l/n jest rozbieżny. SZEREG HARMONICZNY. Szereg liczbowy postaci

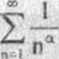
nazywamy szeregiem harmonicznym rzędu a. Na przykład szeregi

są szeregami harmonicznymi odpowiednio rzędu: a = !, a ~ 1/3, a = -3.

Szereg harmoniczny rzędu a £ 0 jest rozbieżny, gdyż nie spełnia warunku koniecznego zbieżności W przykładzie 2,3 wykazaliśmy, ze szereg harmoniczny rzędu a = 1 jest rozbieżny, Można udowodnić (por. rozdz V, 3, przykł. 3.6). źc

a>l szereg    jest zbieżny,

a ś 1 => szereg ^ jest rozbieżny.

sii rozbieżne, a szeregi

Stąd oraz z twierdzeń 21 i 2.2 wynika, że szeregi

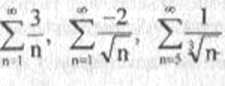
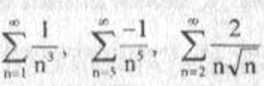
s;i zbieżne.

WARUNKI WYSTARCZAJĄCE ZBIEŻNOŚCI 1 ROZBIEŻNOŚCI SZEREGÓW O WYRAZACH NIEUJEMNYCH

KRYTERIUM PORÓWNAWCZE (zbieżności i rozbieżności

on    <r>

szeregów) Załóżmy, że wyrazy szeregów £a_n, £b_n spełniają warunek

n=-I n 1

0 £ a_n £ b_B dła każdego n e N.

Wówczas

iO    X*.

(1)    Jeżeli szereg £b„ jest zbieżny, to szereg £a_n jest zbieżny.

n=l    n-l

V)    tn

(2)    Jeżeli szereg £a_n jcsl rozbieżny, to szereg £b_n J^esl rozbieżny.

n=l    n=l

D o w ó d Ponieważ twierdzenia (ł) i (2) są twierdzeniami przeciwstawnymi, więc wystarczy' udowodnić jedno z nich. Udowodnimy (l). Przyjmujemy oznaczenia.

S„ = a_l+#_J+-+a„. T„ = b₁ + b,+"-+l>„ neN. (S_n), z uwagi na założenie a_n £0, jest ciągiem niemałejącym, a więc monotonicznym Ze zbieżności szeregu £b_n wynika, że ciąg (T_n) jest zbieżny, a więc ograniczony Zatem istnieje taka liczba M, że T_n < M dla neN. Stąd i z założenia, żc 0 ś a„ £ b„ mamy

. 0 £ S S T £ M,

a więc 0 <> S₀ ś M dla n e N, co oznacza, zc ciąg (S_n) jest ograniczony. Ciąg (S_n), jako monofoniczny i ograniczony, jest zbieżny, a zatem szereg £a_n jest zbieżny .