78142 MATEMATYKA050

92 II. Ciągi i szeregi liczbowe

. . A .. ,1 . 1 , _Ł. _ .    .

Na przykład ciągi (~ + i), (- + i-y) są zbieżne i mają granice n n n

odpowiednio: i oraz 0, natomiast ciągi (n + i) oraz (n + — i) są rozbieżne.

PRZYKŁAD 3.1 Obliczymy granice:

1

. ni + 1    ..    ¹⁴ _n i

^{a)    ,,m}ńTóT ^{= hm}-----o ⁼T ^{= ,ł}

l + l -n

b)    lim(-^—^)*ⁿ = lim(l + -)*" = e"' =cos7t + i$in;t = -l, ⁿ x« n* n **> n

c) lim

n^J +i

1

, =lim(l + i— ) = 1,

n    n    n »•*    fi

n-n²i .. ,1    ..

— = hm(-~i) = -i, i n

i 2"

d) lim

n m> n‘

rn+l _ • />n    9

c) lim———=lim(5-i(_T)^R)=5.

SZEREGI o WYRAZACH ZESPOLONYCH Definicje szeregu, sumy częściowej szeregu, szeregu zbieżnego, rozbieżnego, zbieżności warunkowej i bezwzględnej szeregu o wyrazach zespolonych są dokładnie takie, jak dla szeregu o wyrazach rzeczywistych.

Ta sama uwaga dotyczy również kryterium Cauchy'ego i d'Alcmbcrta dla szeregów o wyrazach dowolnych

Jeśli wyrazy szeregu zapisane są w postaci kartezjańskiej, można stosować następujące twierdzenie:

TWIERDZENIE 3.2 Szereg £a_n o wyrazie ogólnym postaci a_n =a_n+ip_n jest zbieżny wtedy i tylko wtedy, gdy szeregi £a_n oraz £(3_n są zbieżne, przy czym

(Ź(a_B + iP^ = A+iB)o(f]a„=A a £p„ = B).

n»1    n*l    n*l

Jeśli więc szereg ]Ta_n lub vp_n jest rozbieżny, to również rozbieżny jest szereg £a_n.

Na przykład szereg £(-?+(-1)"*-) jest zbieżny, ponieważ

n    n

n~ n

szeregi £-r ^oraz Z(“0°— są zbieżne, natomiast szereg £(— + —) jest

rozbieżny, ponieważ szereg jest rozbieżny.

n

•)Z

*>I

-2^n4,-6i b) I-j=-,

n*l li

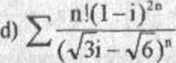
PRZYKŁAD 3.2 Zbadamy zbieżność szeregów: 3-t-2m

n^J ’

n² + 3n (3 + 4i)ⁿ *

a)    Wvrazy tego szeregu zapiszmy w postaci kartezjańskiej:

3 .2 a_n =~r + l —.

" n² n

2

Ponieważ szereg £- jest rozbieżny, więc badany szereg też jest rozbieżny (tw. 3.2).

b)    Wyrazy tego szeregu zapiszmy w postaci kartegańskiej:

\ = ~-2i(|)ⁿ.

»    2    4    2

Szereg Z2(-r)ⁿ jest zbieżny jako geometryczny (a = -r, q = •-), przy n-l    i    ii

a    “>    6

czym jego suma jest równa A = --= 4. Analogicznie, szereg £— jest

1“^    ml3ⁿ

szeregiem geometrycznym (a = 2, q = -j) zbieżnym i ma sumę B = 3.

Zatem badany szereg jest zbieżny i ma sumę równą

S = -Ai - B = -3-4i.