61335 MATEMATYKA036

64 II. Ciągi i szeregi liczbowe

Niżej wymieniamy wszystkie symbole nieoznaczone

^i x —oo, oc-0, q, O ,    ⁰⁰ ,    1

Na przykład ciągi

(n²-3"), (n^!3 "), «n² + l)^v"). ((H-2/n)") są symbolami nieoznaczonymi odpowiednio typu: oc-oo, Ooo, <x>°, T.

W przypadku symboli nieoznaczonych obliczanie granic jest utrudnione, gdyż nic można bezpośrednio stosować wcześniej poznanych twierdzeń. Ciągi, które są symbolami nieoznaczonymi należy najpierw, stosując odpowiednio dobrane do ciągu i do rodzaju symbolu nieoznaczonego przekształcenie, zapisać w takiej postaci, by twierdzenia te mogły być zastosowane.

PRZYKŁADY OBLICZANIA GRANIC CIĄGÓW

PRZYKŁAD 1.3 Obliczymy granice:

,s/n-2"“ 1-0 1

a)    lim-■■/“---■ — . , — ~z >

i>-***> J +    14* 1    2

b)    limn⁶-n^? = {oo°} = lims/n⁶(2—-) = hm(y/n)⁶-y2-— = 1 ;

n-*o>    n-rrj \    n o-**    V n

c)    lim—— = 0. Wynika to z nierówności    i twierdzenia o granicy

b-w n    n n n

trzech ciągów.    ®

PRZYKŁAD 1.4 Obliczymy granice:

a) lim -ⁿ--, ^ = {—} = lim

1-1

"-♦®3n²-fn    ^x* •*-**> ^ ^

n

_H_ =

1-0 1

b)Iim

34-0 3 * 2°..;.+ 4°

2°"« +2²ⁿ x. ..    - ₂

... —--— = {—} = lim ——-

><« 3ⁿ ą. 4° OO •»-** 3ⁿ+4ⁿ

c) lim(n+ Vn²-n)= {+004-00} = oo ;

n+<r>

— (3)* _{+ 1}    ⁰⁺¹

,v . ,    n—; . V (n->/n^J-n)(n+\n“_m_) ₌

(I) lim(n-vn -n) = {+00-00} = lim---—/

n M>    ».-    n+vn^J-n

lim

n^: -(n^J -n)

= lim

n + Vn‘-n

n+Vn²-n

^{«^>=^ TT T+TTTó 2'

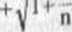
PRZYKŁAD 1.5 Obliczymy granice:

;i> hm(l-V = {r}= Hm [(1--) "iW¹;

b)    lim(-J—•)*" ={r} = lim ⁽¹~"~ = ^ = e ⁴ ;

«-"> ^{n +} l    ^{1 J} " ”>/₁₊1)2» C

n ■

c)    lim(^-^)ⁿ ={2^x} = +oo;

n-»<r. _n + 1

d)    lim(l + 4)" = {r} = lim((l + 4cf*)' = (e²)° =¹ •

n w* n    n*/2

PRZYKł-AD 16 Obliczymy granice:

a)    lim(3 ⁿ + 2^n+l) = {0 + oo} =+ao;

D-M>

b)    Hm(2 + ln-4) = j2. In(0+)| = {2-oo} =-«=, n-*<« n + 3

2    3 o    3

c)    lim(~arctg(2 + n^:) + -^—)= {-arctg(+*>) f rj)- ^{1 f0}~ ¹

7U    n“ +3 TC    ^

d)    lim(n -n² In n) = lim n(l - nln n) = {(+co)(-x)} - ⁰⁰•

lt-*»    n »*e

ZADANIA DO ROZWIĄZANIA

1.    Podać przykład ciągu: a) rosnącego, b) niemalcjącego, c) ograniczonego z góry', d) rosnącego i ograniczonego, e) geometrycznego zbieżnego.

2.    Podać przykład ciągu: a) zbieżnego do 1, b) zbieżnego do 2. c) rozbieżnego do -f-oo, d) rozbieżnego, który nie ma granicy niewłaściwej,