08

^r

Współrzędna poprzeczna środka masy pustego statku powinna być równa zeru, to znaczy środek masy pustego statku powinien leżeć w płaszczyźnie symetrii.

4. Masa i współrzędne środka masy załadowanego statku

Masę statku, na którym rozmieszczone są ładunki w ładowniach (ewentualnie na pokładzie) oraz zapasy i balasty w zbiornikach, oblicza się jako sumę:

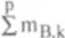
jło«e fal&i n    m

M = Mp + Mj)+ Xni£ j + X m_{s (} +

gdzie:
i	- numer ładunku.
n	- liczba ładunków na statku.
^mC.i	- masa ładunku o numerze i.
j	- numer zbiornika zapasów.
m	- liczba zbiorników napełnionych zapasami.
^mSj	- masa zapasu w zbiorniku j,
k	- numer zbiornika z balastem.
P	- liczba zbiorników z balastem.
^mB.k	- masa balastu w zbiorniku k.

Obliczenia masy statku dokonuje się w tabeli.

Współrzędne środka masy załadowanego statku i Lq obliczane są z równań momentów statycznych mas względem płaszczyzn odniesienia.

Równanie momentów statycznych ntas Dla układu w- spoczy nku, składającego się z kilku elementów, suma momentów statycznych (względem dowolnej płaszczyzny odniesienia) mas elementów składowych układu równa jest momentowi statycznemu masy całego układu. Można to zapisać za pomocą równania matematycznego:

n

M w = £(mj Wj)

i-l

gdzie:

M = £mj - masa układu.

i=l

w - odległość środka masy układu od płaszczyzny odniesienia (w = x, y lub z).

i - liczba elementów układu, m, - masa elementu układu.

Wj - odległość środka masy elementu i od płaszczyzny odniesienia (w* « y* lub z,).

Równanie momentów może być stosowane również dla innych niż masa wielkości fizycznych, na przykład dla siły, powierzchni i objętości. Korzysta się z tego na przykład obliczając środki powierzchni lub objętości skomplikowanych figur płaskich lub bry ł

W odniesieniu do statku, dla układu współrzędnych związanego z nim, równania momentów statycznych mas i wyrażenia na współrzędne środka masy statku mają postać:

M xo = M_P XGP+I(mi Xj)

i=l

M zg = M_p zqp+ I(mj Zj)

i=l

^XGP+ I(^mi *i)

_12J_

M

M_P z_GP+ I(m, z,)

_isJ_

M

13