138 139 (3)

Uti

Przestrzenie euklidesowe

b) Oznaczmy symbolami t>i, i2, v₃ kolejno generatory przestrzeni Eq. Jest to baza ortogonalna tej przestrzeni, gdyż (vj, v?) = (Si, 5₃) = (*₂, £3). To oznacza, że

lu «i) ^    ( u, v₂) _ (tt, v₃),

«C = ,, J - _|2 1>I 4 —_-^T *2 +    ^v3

!ł^t?i li

c) Bazę ortonormalną przestrzeni stanowią tu wektory <?i, 03. es należące do bazy standardowej przestrzeni E^s. Szukamy rzut ma zatem postać

tio = («. €i)«j 4 (u, e₃) e₃ 4 [*, e_£) e₅ = [1,0, 3,0,5).

dl Oznaczmy g_x = J, g₇ = sin 2x Oczywiście X g₂ więc. szukany rzut f_c funkcji / obliczamy ze wzoru

sin 2z.

iis.r ii9.ii

e) Niech q_t = r — 1, <y₂ = S*² — 5z 4 1 Łatwo się przekonać, ze (q_x, q₇) = 0. Rzut ortogonalny p₀ wielomianu p ma więc postać

^Po=HF^,,+ iftTr^{łł =} ^~¹⁾⁺?^{(3t5_6l + l)s0}-• Przykład 14.4

Stosując macierzowy wzór na rzut ortogonalny znaleźć rzuty ortogonalne w odpowiednich przestrzeniach 2T podanych wektorów' u na podprzestrzeń

lin {«i, t?2, • ■ 1 ®fc} :

a)    u =(10,2 1), 5, =(1,1,2) ć₂ = (1, 1,-2);

b)    u = (1,4,0, —2), 5, = (1,1,0,2), V2 = (1,0,1,0), S₃ = (0,1,2,1).

Rozwiązanie

Niech A będzie macierzą wymiaru m xn o liniowo niezależnych wektorach kolumnowych. Wówczas rzut ortogonalny w przestrzeni E'⁷¹ wektora kolumnowego fi na podprzestrzeń rozpiętą na kolumnach macierzy A ma postać J3q = AXo, gdzie Xq = (./l^r.4) A' B jest wektorem współrzędnych tego reutu w bazie wektorów kolumnowych macierzy A. Wykorzystując powyższy fakt mamy

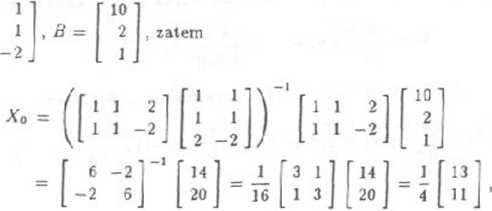
1

a) A =

1

2

Czternasty tydzień --przykłady

- -

więc

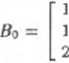
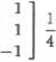
13

11

Rzutem ortogonalnym jest więc wektor Uę = (6,6,1).

b) A =

110"		' 1 '
1 0 1	II	4
0 1 2		0
.201.		. -2 .

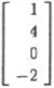
, zatem

Rozwiązanie

Niech AX = B będzie sprzecznym układem m równań liniowych z n niewiadomymi, przy czym rz A = n. Przybliżone rozwiązanie Xo tego układu równań wyznaczamy metodą najmniejszych kwadratów w taki sposób, aby wektor AXq £ E^m znajdował się najbliżej wektora B 6 £¹ⁿ. Będzie tak, gdy wektor AXo będzie rzutem ortogonalnym wektora B na podprzestrzeń generowaną przez wektory kolumnowe macierzy A. Metoda ta ma praktyczne zastosowanie wtedy, gdy z przesłanek fizycznych wynika, że jedyne rozwiązanie układu równań istnieje, zaś przybliżone dane doświadczalne obciążone błędami pomiarów prowadzą do sprzecznych układów równań.

a) Rozważany układ równań jest sprzeczny, zaś rząd macierzy tego układu jest równy liczbie niewiadomych. Przybliżone rozwiązanie (zo.yo) tego układu wyznaczamy jako współrzędne rzutu ortogonalnego io wektora u = (5,4,1) na podprzestrzeń V genero-

X₀

('1102' 10 10

.0121.

110"	\
l 0 1
0 1 2
2 0 1 J	/

110 2 10 10

0 12 1

	'6	1	3 '	-i	' 1 '	1	' 8	0	-4 '		' 1 '	1	' 0'	_ 1	'0'
_	1	2	2		1		0	27	-9		1		9		1
	.3	2	6 .		. 2 .	“ 35	. —4	-9	11 .		.2 .	36	.9.	~~ 4	. 1.

więc

Bo =

'110'		r n i		' 1 "
1 0 1	1	u 1	_ 1	1
0 1 2	4	. 1 .	“ 4	3
to o				1

Rzutem ortogonalnym jest więc wektor Ud =

l 3 1 U 4¹4¹4

)■

f X + 2y = 2 c) < 2x -f y = 8 [ 3x + y = 1

(2x - y = 5 a) < x + 3y = 4 ; [ 3x + 2y = 1

(x + z =    1

y + ¹ = -i .

X - y + z =    0 ¹

z= 1

1

Przykład¹ 14.5

Metodą najmniejszych kwadratów znaleźć przybliżone rozwiązania podanych układów równań