144

144

Egcs - najmniejsza odchyłka średniej stałej cięciwy zęba, mm;

Escs~ f (średnia średnica podziałowa dm, kąt stożka podziałowego 6, średni moduł ) (tabl. 12.1.10);

Ts_C - tolerancja średniej stałej cięciwy zęba, mm;

Tśc~ f (rodzaj tolerancji luzu bocznego, F_r) (tabl. 12.1.11);

F_r (tabl. 12.1.5).

k_r - współczynnik dla określenia wartości Eś cs przy różnych klasach dokładności (tabl. 12.1.12).

Najmniejsza odchyłka średniej stałej cięciwy zęba E_scs jest określona tylko dla rodzaju pasowania H i klasy dokładności 7. Dla określenia Escs w innych klasach dokładności i rodzajach pasowań, wartości E_scs mnoży się przez współczynnik k_r. Przy pomiarze grubości zębów na zewnętrznym czole kół najmniejsza odchyłka średniej stałej cięciwy zęba Eścs i tolerancja T_śc zwiększa się w stosunku [(tf_e-0,5b)/*_e].

2. Wysokość pomiarowa - wysokość głowy zęba do zewnętrznej stałej cięciwy (h_c>), mm, odpowiadająca nominalnemu położeniu zarysu odniesienia

kcc—h_ac~ 0,1607 *S>t(2),

gdzie: h_ae - zewnętrzna wysokość głowy zęba, mm:

-dla zębnika h_ae\ = (A*+*i)/n_te;

- dla koła zębatego h ael “ (2ha mte-h OCl)j ha = 1,0 - współczynnik wysokości głowy zęba.

PRZYKŁAD 4. Koło stożkowe z₂= 32, m_te- 5 mm, /? = 0°,

klasa dokładności 8—C, *!=+(),3, (x₂=-0,3), ^xt\~ 0, R_e=93,04mm, 6= 25 mm, ó=59°18\

Em — Rg - 0,5 b = 80,54 mm;    (rys. 12.3.17)

d_e-m_tez₂= 532 = 160 mm; d_m=d_eR_mIR_e= 160-80,54/93,04= 138,50 mm; m_m = m_te R_m/R_c - 5 • 80,54/93,04 = 4,33 mm;

5_el ==(1,571+0,728*1+jr_n)/n_te = (1,571+0,728 0,3+0)-5 = 8,947 mm;

Sc2~ n    Se i ~ 3,1416 -5-8,947 = 6,761 mm;

Egęg~ 0,03 mm (tabl. 12.1.10) {m_m = 4,33 mm, <5 = 59° 18',

d_m = 138,50 mm);

A>=3 (tabl. 12.1.12) (klasadokładności - 8-C);

F_r - 0,071 mm (tabl. 12.1.5) (klasa dokładności - 8, d_m= 138,5 mm,

m_m = 4,33 mm);

Tabl. 12.1.10. Najmniejsza odchyłka średniej stałej

cięciwy zęba E_scs    pn-so/m-88522.03

Klasa dokładności	Rodzaj pasowania	Moduł średni m m, mm	Średnica podziałowa d, mm
			d	m <125		125<rfm<400			400< dm $800
			Kąt stożka podziałowego, ó °
			<20	20 < <45	>45	<20	20 < <45	>45	<20	20 < <45	>45
						F ś cs >
		1 s ^m ni < 3,5	20	20	22	28	32	30	36	50	45
		3,5^ mm<6,3	22	22	25	32	32	30	38	55	45
7	H	6,3 < Qim< 10	25	25	28	36	36	34	40	55	50
		10 $ 16	28	28	30	36	38	36	48	60	55

Tabl. 12.1.11. Tolerancja średniej stałej cięciwy zęba T_sc

PN-80/M-88522.03

c? y	Dopuszczalne bicie promieniowe uzębienia Fr,
•Sg	>20	>25	>32	>40	>50	>60	>80	>100	>125	>160
3 &	$25	$32	<40	$50	$60	$80	$100	$125	<160	$200
3					Tśc ,
h	32	38	42	50	60	70	90	110	130	160
d	42	48	55	65	75	90	110	130	160	200
c	52	60	70	80	95	110	140	170	200	260
b	65	75	85	100	120	130	170	200	250	320
a	85	95	110	130	150	180	220	260	320	400

Tabl. 12.1.12. Wartości współczynnika k_r

określającego E_ścs dla różnych klas dokładności

PN-80/M-88522.03

Rodzaj pasowania		kr
	Klasa dokładności dotycząca płynności pracy
..	6	7	8	9
H	0,9	1,0	—
E	1,45	1,6	—	—
D	1,8	2,0	2,2	—
C	2,4	2,7	3,0	3,2
B	3,4	3,8	4,2	4,6
A	5,0	5,5	6,0	6,6

Tś_C= 0,11 mm (tabl. 12.1.11) (F_r = 0,071 mm, pasowanie - C); Eś*cć=E_ścs k_r [R _e fR_m ] = 0,03 3 [93,04/80,54] = 0,104 mm; Ts\= T_śc[Re/Rn,h 0,11 [93,04/80,54] = 0,127 mm;

5^ = 0,883 5_c2 = 0,883-6,761 = 5,970 mm;

Śce = (Sj-Eś*ce) -Tsl = (5,970-0,104)_8_t[27 = 5,866 _S,₁₂₇ mm.

h_ce = (1,0 + 0,3) - 5 - 0,1607 -6,761 = 5,414 mm.

12.1.3.2. GRUBOŚĆ ZĘBA WZDŁUŻ ŚREDNIEJ STAŁEJ CIĘCIWY S_c

I WYSOKOŚĆ POMIAROWA ZĘBA h_c

1. Grubość zęba wzdłuż średniej stałej cięciwy ( S_c)

- długość cięciwy odpowiadająca grubości nominalnej zęba w średnim przekroju (rys. 12.1.5).

Grubość nominalna zęba wzdłuż średniej stałej cięciwy, odpowiadająca nominalnemu położeniu zarysu odniesienia, mm    Ś_c 1(2)= 0,883 Snm\&)>

gdzie 5^1(2) - grubość zęba zębnika (koła zębatego) po

podziałowej średnicy d_ml{2) w średnim przekroju zęba, mm;

Snw\ = (1,571+ 0,728 Xi+AV])/nj, - dla zębnika;

S_nm2 = (7T/n„- Snm i) - dla koła zębatego.

Rzeczywista grubość zęba wzdłuż średniej cięciwy (podawana na rysunku wykonawczym koła), mm;

5_CI = (S_cJ -E_scs,)-T_ści - dla zębnika;

Ą₂= ( S_c\-Eścs2)-T_ŚC2 - dla koła zębatego,

2a

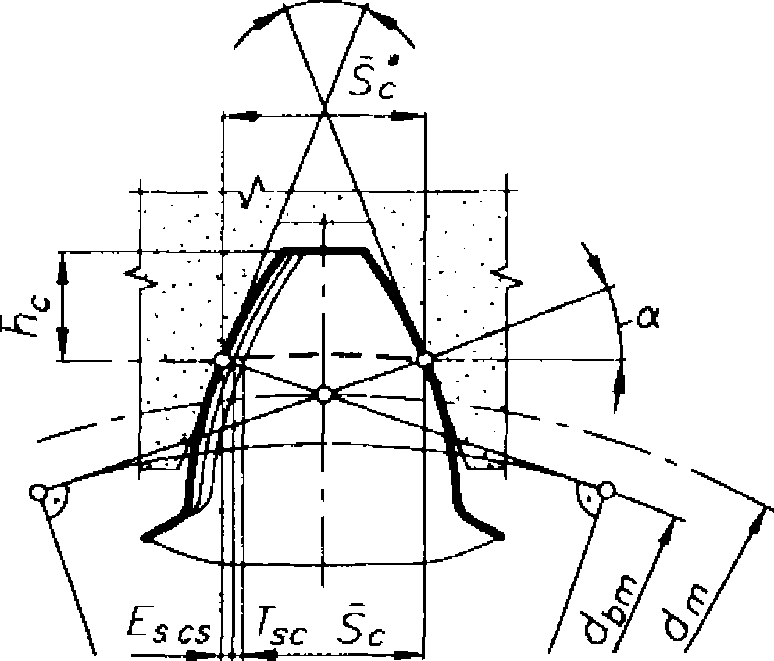
Rys. 12.1.5. Schemat pomiaru grubości zęba wzdłuż średniej stałej cięciwy oraz odchyłki i tolerancje grubości dla kół stożkowych o zębach kołowych

__