2011 12 19";58;444

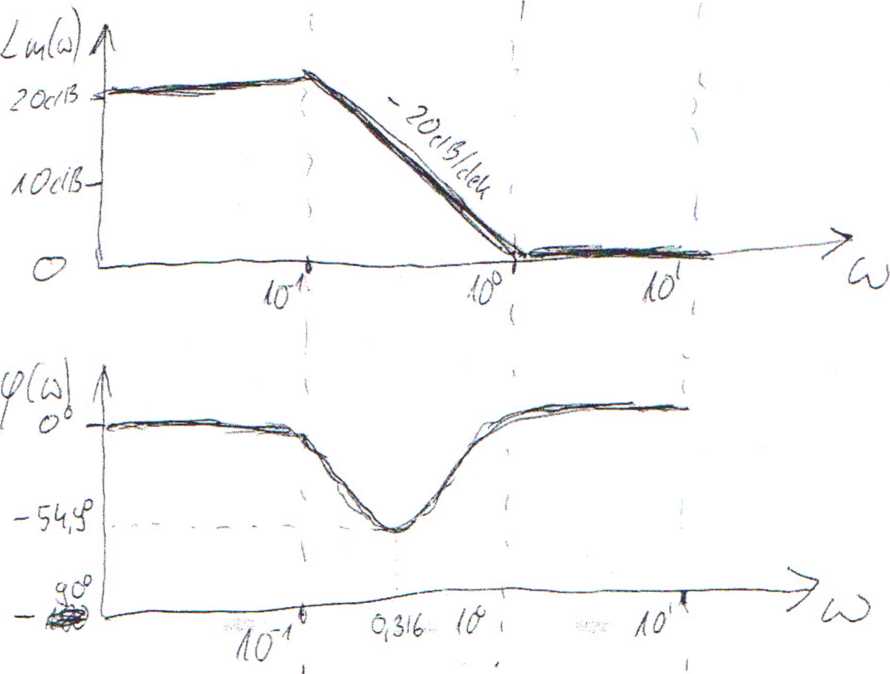
• ^dla u;<0.1 = 10 ¹    Lm(u)£z'2Qlogl0 + 20log'i/i — 2Qlog\fi = 20dJ3

•    ^d|au><l = 10° Lm(uj)zi^t20logl0+2Qlog\/i~-2Qlog\J(l0uj)² =

= 20 db + OdB —[20%^ + 20/op^] = - 20%u;

• dla ^>1 = 10°    Lm(w)« 20toff 10 + 20- 7Qfog\/(10w)² =

= 20d& + 20 log\fcź -[20logsf\tf + 20log\[wi] = OdB

Do <p(w) najlepiej podejść zdroworozsądkowo - na egzaminie się bałem, że to co mi wychodzi to herezje i nie narysowałem, ale to jest dobrze. A więc patrzymy na wykres funkcji y=arctg(x):

•    Dla wartości x bliskich 0 zarówno arctgx jak i arctglOx będzie bliski 0, a więc (arctgx - arctglOx) też będzie ok. 0.

•    Dla dużych wartości x mamy arctgx w przybliżeniu równy arctglOx, a więc (arctgx - arctgl0x) też będzie ok. 0.

•    Gdzieś pomiędzy przegięciami funkcji Lm nasza funkcja "urośnie" do minus "iluś tam" stopni.

I