2011 12 19";58;443

Zadanie 5

Dla układu z zadania 4 zaprojektować korektor opóźniający, taki aby uchyb ustalony położenia był mniejszy od 5% (0.05).

Rozwiązanie

Tk#+\

TF*+1

Korektor szeregowy ma ogólną postać:

wyznaczanie A

Transmitancja układu z korektorem:

_n ( V    2 _tTk* +1

^g»(*) = 5

53 + 35'2 + 35 + l

■A'

2A!T*5+2A

Uchyb układu z korektorem:

U(s)

E(s)

1 + Go(5)

1

5

^5 + 1    (53+ 352+ 35 + 1) (^5 + 1)

2ATks+2A

(53+35'2+3a+l)(^s+l) (53 + 352 + 35 + 1) (§5 + 1)

Tfk,

(53+3s2+3a+l) (~s+1)+ 2AT_ks+2 A Uchyb ustalony układu z korektorem:

n    (53 + 352 + 35+ 1){^5+1)

E_u(s) = lim = lim

s-+0 1

2A + 1

•° ⁹ (53 + 352+35 +1)(§5 +1)+ 2ATa-5+2A

Jeśli uchyb ustalony ma być równy 0.05, to:

drrŁ* ^A=19/2

- wyznaczanie a

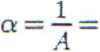
2

19 - wyznaczanie Tk