3 M1 DohnalJ MatusiakK ZAD33

1x0=709242,45 [mm4]
Iy0=ly01 + Iy02
10 *1203
y01 12 50 * 203
= 1440000 [mm4]
y°2 12
Iy0=147333,33 [mm4]
= 33333,33 [mm4]
IxO=Ir
Iy0=I
max
2. Obliczenia smukłości pręta.
a) Długość wyboczeniowa lw=l*|i=2000*l=2000 [mm]
b) Minimalny promień bezwładności
Imin
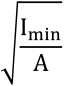
1709242,45
J 2200
17,96 [mm]
c) Smukłość rzeczywista
s =
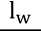
Imin
2000
17,96
111,36
d) Smukłość graniczna
s
gr
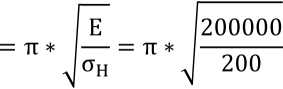
99,35
s > sgr wyboczenie sprężyste - stosujemy wzór Eulera 3. Obliczenie siły krytycznej.
Fkr ~
n * E * L
l2
n* 2 * 105 * 709242,45 20002
349997,12 [N]
3
Wyszukiwarka
Podobne podstrony:
3 M1 DohnalJ MatusiakK ZAD38 3. Przypadek c. a) Obliczanie minimalnego promienia bezwładności. ^min
3 M1 DohnalJ MatusiakK ZAD310 d) Sprawdzenie warunku s < sgr wyboczenie niesprężyste — stosujemy
3 M1 DohnalJ MatusiakK ZAD311 h) Obliczanie siły dopuszczalnej FLp = °doP * A = 43,31 * 2790 = 1208
3 M1 DohnalJ MatusiakK ZAD32 Rozwiązanie: 1. Obliczenie momentu bezwładności pręta. 120 Ai a2
3 M1 DohnalJ MatusiakK ZAD34 4. Obliczanie siły dopuszczalnej. 349997,12 ---= 69999,42 [N] * 70 [kN
3 M1 DohnalJ MatusiakK ZAD36 Rozwiązanie: 1. Przypadek a. a) Obliczanie minimalnego promienia
3 M1 DohnalJ MatusiakK ZAD37 2. Przypadek b. a) Obliczanie minimalnego promienia bezwładności. Ir 1
3 M1 DohnalJ MatusiakK ZAD39 b = 4^5 = °’007 [MPal aJk° = 240 - 0,007 * 82,022 = 192,91 [MPa] f) &n
więcej podobnych podstron