4560

146 Gćomotiin nnnlityczna w przostrzoni

normalnym fi jest określona wtórem

1*1 v\

Ponieważ prosta / nu wektor kierunkowy fl s? (-3,-2,1), a płaszczyzna » wektor nor-malny fi =s (2,-3,0), więc

arccos

UROI

Ig,-3,0) x (-3,-2,1)|    _

sA-3)⁵* + t-²)² + l^av/2³+3*-HH K—3,—2,—13)| l4-yfi3

arccos 1 = Ofrad j.

oznacza to, że prosta I jat równoległa do płaszczymy r.

b) W tym przykładzie wykorzystamy fakt mówiący, te miara kąta między dwiema płaszczyznami jest równa mierze kąta między wektorami normalnymi tych płaszetytn. Wymarzymy teraz wektory normalne płaszczyzn r, i -z- Płaszczyzna x, jest rozpięta na wektorach i. = (-1,2,0), $i = (1,1,1). a płaszczyzna rj na wektorach i₃ = (0.1,-3), h = (l.o,-2). Wektory normalne ii: i "z ty<* płaszczyzn mają odpowiednio postaci:

i,, i, x 5, =(-1.2.0)x(l,l,l) = (2.1,-3), n, = i, x V2 = (0,1, -3) x (1.0, -2) = (-2,-3,-1).

Miara kąta o między wektorami normalnymi fi: i «a (a zatem i między płaszczyznami *: i za) jest równa

arccos

|«i o izl

li.l-TO

1(2,1,-3) o (-2, -3,-1)1 — arccos    —2    ==

W + P + (-31* • v/(-2)» + (-3)’ + (-!)’

x + y —1 = 0,    RM

y-z + 3-0    "^{,a P0Sli}*

= arccos - as 1,28(rad]sa 73,4*. c) Kątem między dwiema prostymi nazywamy kąt między wektorami kierunkowymi tych prostych. Wektor kierunkowy vi prostej U :

5, = (1,1,0) X (0,1, -!) = (-!, 1,1),

wektor kierunkowy prostej /» : j lj+3^+₂z = 0 ^posłać

h = (1,-2.1) X (-1.3,2) = (-7,-3,1).

Miara kąta o między wektorami ii i (a zatem i miara kąta między prostymi li i h) jest równa

o

arccos

|g» o Sal

i®i l • IWi

------ |(-1.1.1) O ("7,-3, Dl

\A-l)^a + 1^J + 1* %(-7)> + (-3)* + 1*

as 1,19 [ rad ] as 67,9°.

= arccos

Trzynasty tydzień • przykłady    .....

• Przykład 13.3 Wyznaczyć rzut prostokątny:

a)    punktu P = (1,0, -3) na prostą I: - ₌ ^v ~ 1 _ z + 1

b)    punktu P = (0,0,1) na płaszczyzną jr:x + y_₂z + 4-o-e) prostej/: r = ys z na płaszczyznę x_: x + 2y + 3_r _ ^ ‘

Rozwiązanie

a) 1 sposób. Punkt P € I jest nutem prostokątnym punktu P na prostą I, jeżeli spełniony jest warunek

P'P1 v,

gdzie » oznacz a wektor kierunkowy prostej /. Niech P = (r, y, r). Wtedy

P P= (1—x,—y,—3 — *)

Wektor P'P jest prostopadły do wektora 5 = (2,-1,2) wtedy i tylko wtedy, gdy P'P o v = 0. Współrzędne punktu P spełniają zatem układ równań

{* _ y-i _ z + i

I 2    -1 ' 2 *

J (1 ~ x, -y,-3 - e) o (2,-1,2) = 0.

Układ ten jest równoważny okładowi

{-* - 2, = -2.

2y + z =    1,

-2* + j - 2r s 4.

-j. Zatem

Rozwiązaniem tego układu jest trójka liczb z = — jj, y = 12, ;

/ 2 10 11 \ ” V 9' 9 ‘    9 /'*

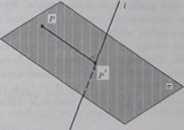
II sposób. Szukany rzut P jest punktem, w którym prosta I przecina płaszczyznę s prostopadłą do niej i przechodzącą przez punkt P. Równanie płaszczyzny ma postać

w: 2r - y + 2« + 4 = 0.

Prostą / przedstawiamy w postaci parametrycznej

I: * m 21, y m 1-1, r - -l+2(, gdzie t € R-

Współrzędne punktu /»' = (21.1 - 1,-1 + 21) wyznaczamy z zaleinoki 2(21) - (1 -0 + 2(— 1 + 2f) -|- -1 = 0.