9

1 Przy zastosowaniu transformacji Hetmana jako transformacji korekcyjnej, kąt skręcenia a będzie na cgói kątem na tyle małym, źe słuszne staje się uproszczenie ces(a) » 1 oraz sin {a) u przenoszona cdpowieomo na w2ory transformacyjne.)

Jednym z elementów kontrolnych transformacji Hetmana (można to zastosować na etapie testowania procedur komputerowych) jest sprawdzenie równości miar kątów odliczanych raz ze współrzędnych pierwotnych i drugi raz ze współrzędnych po transformacji (7.10). Odpowiadające miary długości powinny natomiast spełniać proporcje stosownie do skali m.

7.4.2. Korekta posttransforrnacyjna Hausbrandta

Współrzędne otrzymane z transformacji według wzorów (7.10) nie muszą się pokrywać z analogicznymi współrzędnymi punktów dostosowania, które jako wielkości dane służyły do wyznaczenia współczynników (parametrów) transformacji. O rozbieżnościach w tym zakresie świadczą wielkości poprawek, obliczane według wzorów (7.11). Aby nie powodować zmian w dotychczasowych współrzędnych (jako danych archiwalnych) prot. Hauebrandf) zaproponował pewnego rodzaju dodatkowe ..uzgodnienie' współrzędnych, zwane tu korektą posttransfcrmacyjną. Polega ona na tym. że współrzędna punktów dostosowania w układzie wtórnym pozostawia się w takiej postaci, w jakiej były przyjęte do transformacji (można powiedzieć inaczej, że do współrzędnych transformowanych (7.10) dodaje się wartości poprawek (7.11). powracając do wartości współrzędnych katalogowych), natomiast wszystkim pozostałym punktom transformowanym przyporządkowuje się poprawki wyznaczone przy zastosowaniu specjalnych wzorów interpolacyjnych.

(7.15)

(sumowania po /- 1. 2,..., n ;j - wskaźnik punktu transformowanego)

W ten sposób następuje świadome deformowanie wyników transformacji Helmerta, jakkolwiek ma ono pewne cechy regularności.

Jak widać, przedstawione wzory są podobne do wzorów na obliczanie średnich ważonych, gdy wagi są odwrotnościami kwadratów odległości danego punktu o wskaźniku J (w zbiorze wszystkich punktów transformowanych) od punktu dostosowania o wskaźniku / (w zbiorze punktów dostosowania). Ilustruje to przykładowo rys. 7.1. Długości d, obliczamy na podstawie współrzędnych pierwotnych. Wielkości poprawek (7.15) dodajemy do wspóirzędnych po transformacji, czyli do współrzędnych wyznaczonych za pomocą wzorów (7.10).

(Uwaga dotycząca algorytmu obliczeniowego: W przypadku, gdy punkt transformowany jest identyczny z pewnym punkiem dostosowania, wówczas formalnie odległość ety • 0. Celem uniknięcia przypadku nieokreśloności wagi [1/df ) możemy ..obowiązkowo’ do każdej obliczanej długości dodawać małą liczbę dodatnią, np. 0.00001 m, która nie będzie mieć istotnego wpływu na interpolowane wartości poprawek i stanowi lylko numeryczny parametr

'J HĄusofUfiOt Rachunki Geodezyjne (1953J. N.Ed.: Rachunek wyrównawczy i obliczenie goods-zyjne. T. il. PPWK. Warszawa i97t.

regularyzacyjny. Otrzymana odpowiednio duża waga oznacza, za poprawi do współrzędnych danego punktu Dędą się praktycznie równać poprawkom odpowiedniego punkiu dostosowania.}

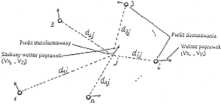
Rys. 7.1. Ilustracja do zadania korekty Hausbrancfta

7.5. Podstawowym zbiorem danych do przeprowadzania iranstormacji korekcyjnych (w sensie globalnym lub (i) lokalnym) są punkty osnów państwowych wyższych klas (rzędów) niż punkty przeliczane, posiadające współrzędne w obu układach, np. .2000' i „1965“ (zbiory współrzędnych są dostępne w ośrcdkacn dokumentacji geodezyjnej i kartograficznej), przy czym w odniesieniu do Interesującego nas obiektu pomiaru (transformacji) wyróżnimy w szczególności:

•    punkty zewnętrzne, jeśli nie są to punkty powiązane obserwacyjnie (bezpośrednio) z obiektem pomiaru (transformacji),

•    punkty wewnętrzne, jeśli wchodzą w skład punktów obiektu transformowanego (sieci). Sytuację ilustruje symbolicznie rys. 7.2.

Punktami dostosowania (punktami łącznymi) transformacji mogą być zarówno punkty zewnętrzne, jak też punkty wewnętrzne obiektu transformowanego. Podstawowym warunkiem na to, by punkt osnowy wyższego rzędu mógł być punktem dostosowania transformacji, jest to, by współrzędne punktu wyznaczone w obu interesujących nas układach (pierwotnym i wtórnym) odnosiły się do identycznego fizycznie znaku geodezyjnego. Taka sytuacja ma miejsce, na przykład, w odniesieniu do sieci I i II klasy. Praktycznie cały obszar kraju, z gęstością charakterystyczną dla punktów 11II klasy jest .pokryty’ tymi punktami i są one lym samym dostępne do wykorzystania w omawianego typu zadaniach. Dla wszelkich nowych obiektów pomiarowych byłyby to więc punkty zewnętrzne. Zauważmy, że punkty takie brane jako punkty dostosowania transformacji nie muszą aktualnie fizycznie istnieć (mogły ulec zniszczeniu) lub mogły zmienić swcje położenie. Ważne jest tylko to. by ich współrzędne zarówno w układzie „1992*, jak też w układzie „1965" były wyznaczone w oparciu o ten sam zbiór obserwacyjny.

W podzbiorze punktów wewnętrznych wyróżnimy ponadto punkty kontrolne. Będą to punkty, które z racji prawdopodobnego przemieszczenia w stosunku do stanu pierwotnego nie mogą formalnie pełnić funkcji punktów dostosowania transformacji. Z taką sytuacją mamy do czynienia zwłaszcza na obszarze strefy 5. gazie

81