badwłasn0045

Jeśli przyjmiemy, że działający moment gnący zmienia swą wartość, toi

• wzrost momentu powoduje zmniejszenie promienia " ^ "

(wzrasta krzywizna) , a tym samym rodnie 6    ,

- zmniejszający moment powoduje wzrost promienia ^ i zmniejszenie naprężenia 6 , gdy g » oo - belka wyprostowana to & m o .

Charakterystycznym przypadkiem wzrostu naprężenia w belce zginanej jest moment, gdySy_maI osiągnie wartość naprężenia na granicy plastyczności 6°    . Oznacza to, że w warstwie dla

któreJ Sy,^ = 6"p    , spełniony jest warunek przejścia materia

łu w stan plastyczny* Dalszy wzrost momentu gnącego będzie powodował rozprzestrzenianie się strefy odkształcać plastycznych, a rozkład naprężenia w przekroju będzie zależał od rodzaju przyjętego schematu ośrodka eprężysto-plastycznego. Hożna tu przyjąćt

-    ośrodek sprężysto-plastyczny bez konsolidacji mechanicznej (Hys. 50 a) ,

-    ośrodek sprężysto-plastyozny z konsolidacją mechaniczną liniową (Kys. 50 b) ,

-    ośrodek sprężysto-plastyczny z konsolidacją mechaniczną krzywoliniową (Rys. 50 c).

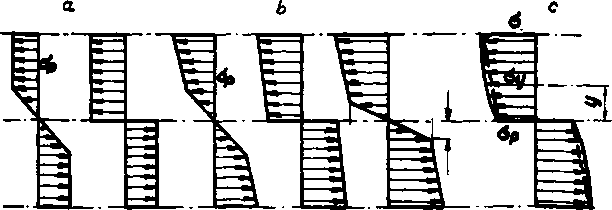
Rys. 50.

Jedli przyjmiemy pewne uproszczenie, ale uwzględniające umocnienie metalu odkształcanego plastycznie, to można rozkład naprężeń, po całkowitym uplastycznieniu przekroju belki, przedstawić za pomocą schematu z konsolidacją liniową, (rys, 51.) .

*

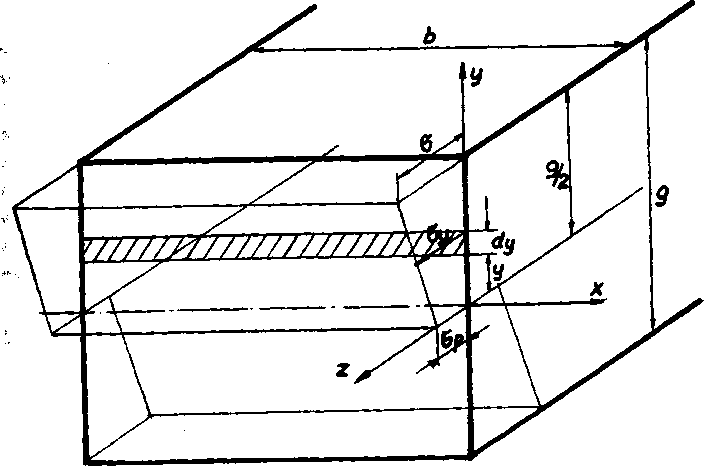
Rozpatrując rozkład naprężeń w prostokątnym przekroju 'belki zginanej plastycznie, wielkość elementarnego momentu 'sił wewnętrznych, działającego względem płaszczyzny obojętnej, wynosi:

cLMpi =    <^-y = dPy

.V