DYNAMIKA0009

WZORY

WZORY

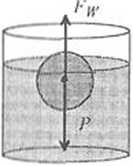
Siła wyporu dla ciała zanurzonego w cieczy wynosi: '•|r"Pc#*V    (2 39)

gdzie: p_c • gęstość cieczy, jf - przyspieszenie ziemskie, F₀ * objętość części ciała zanurzonej w cieczy. Zamiast gęstości cieczy p_c we wzorze (2.39) może występować ciężar właściwy cieczy y_c ■ p_c Oprócz siły wyporu na ciało zanurzone w cieczy działa również siła ciężkości

/* - m# * p tfF,    (2.40)

gdzie: p - gęstość ciała a F- jego objętość. Aby ciało pływało w cieczy siła ciężkości musi być zrównoważona siłą wyporu F =/•„.; czyli:

PX^r = P_t. JT .

Prawo Hookc’n

Jeżeli do pręta, o długości początkowej /„ i powierzchni przekroju poprzecznego S ,\l    zostanie przyłożona siła rozciągająca

• >j—fr- /•' (ściskająca) /•', to pręt ulegnie wydłużeniu -■■ ■■ '    '    ^J ^ —*    * (skróceniu) o A/zgodnie ze wzorem:

^/(ł    .    (2.41)

■’ 'o

gdzie /: - moduł Younjfa, który jest w ielkością charakterystyczną dla materiału pręta Wielkość F/S nosi nazwę naprężenia, a A///₀ - względnego wydłużenia. Dla pręta o ustalonych wymiarach z (2.41) wynika, że:

F~ktJ.    (2.42)

Współczynnik k ■ l:S/l_n nosi nazwę stałej sprężystości Zależność (2.42) opisuje nie tylko odkształcenia pręta, ale dotyczy również innych odkształceń sprężystych (np. przy’ rozciąganiu lub ściskaniu sprężyny).

Rozszerzalność termiczna ciał

Pręt ulega wydłużeniu (skróceniu) o A/ pod wpływem zmiany temperatury o A/:

~ = XAi lub / - /₀( I ♦ XAi).    (2.43)

'o

gdzie l_Q. I - początkowa i końcowa długość pręta, a X • współczynnik rozszerzalności liniowej.

Pod wpływem zmiany temperatury o A/ zmianie ulegają również pozostałe wymiary.

' czyli cała objętość ciała

jr = aAi lub F- (V₀ + oA/)    (2.44)

^vo

gdzie Fy .F - początkowa i końcowa objętość ciała, a a jest współczynnikiem rozszerzalności objętościowej Między obydwoma współczynnikami istnieje zwią- \ zek: a = 3X. Wzór (2.44) dotyczy zarówno ciał stałych jak i cieczy.

53