egzamin2009 1

* . .

L (pkt. 3) Sformułować algorytm przekształcający podaną z klawiatury liczbę naturalną (wprowadzaną jako ciąg cyfr dziesiętnych, począwszy od'najbardziej znaczącej) .na odpowiadającą jej postać binarną i wyprowadzający uzyskany wynik na ekran monitora (w kolejności od najbardziej do najmniej znaczącego bitu). Przyjąć, że po ostatniej cyfrze dziesiętnej będzie naciskany klawisz „ENTER”. Oszacować złożoność asymptotyczną typu 0(.) zarówno w stosunku do czasu wykonywania obliczeń, jak i niezbędnych do rozwiązania problemu zasobów pamięciowych. Rozmiar danych wejściowych scharakteryzowany jest przez wielkość liczby przekształcanej n (rozumianej jako wielkość ^abstrakcyjna, niezależna od sposobu jej prezentacji).

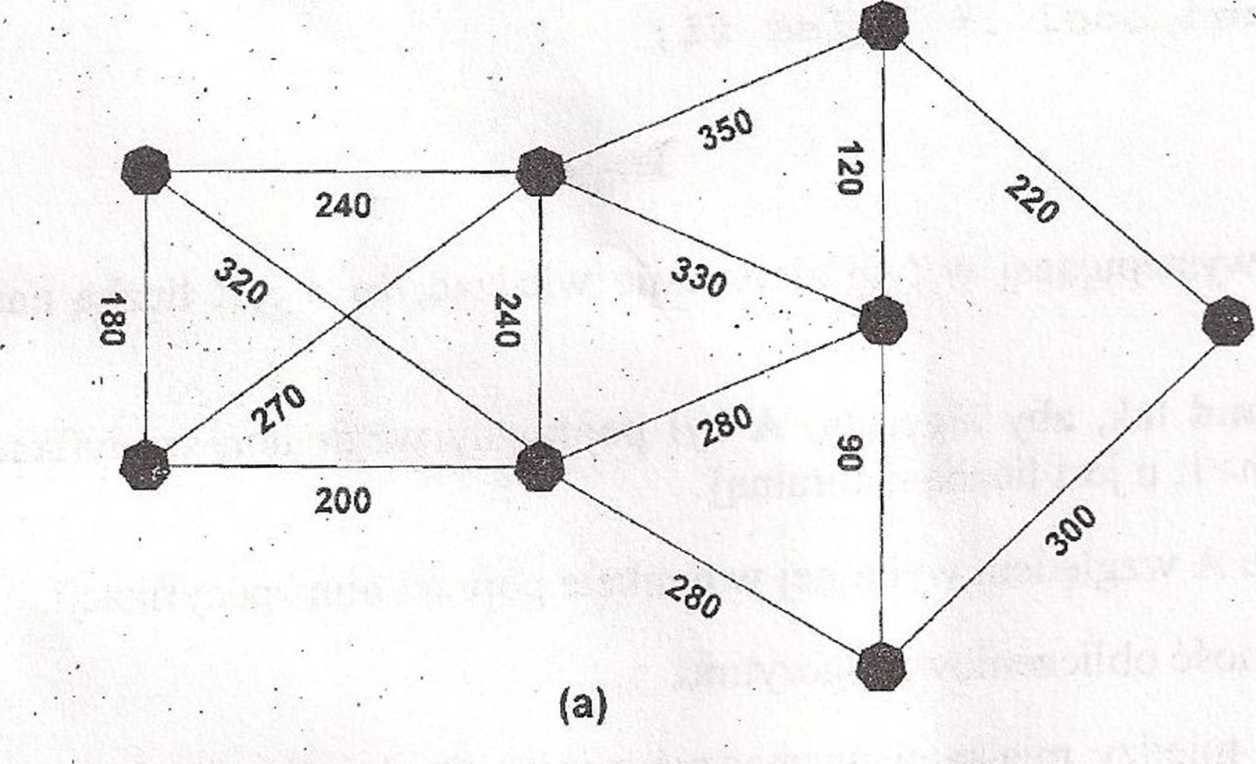
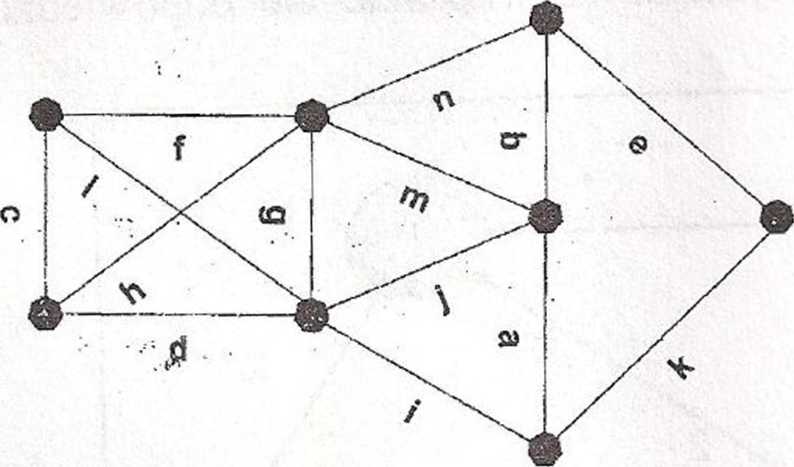
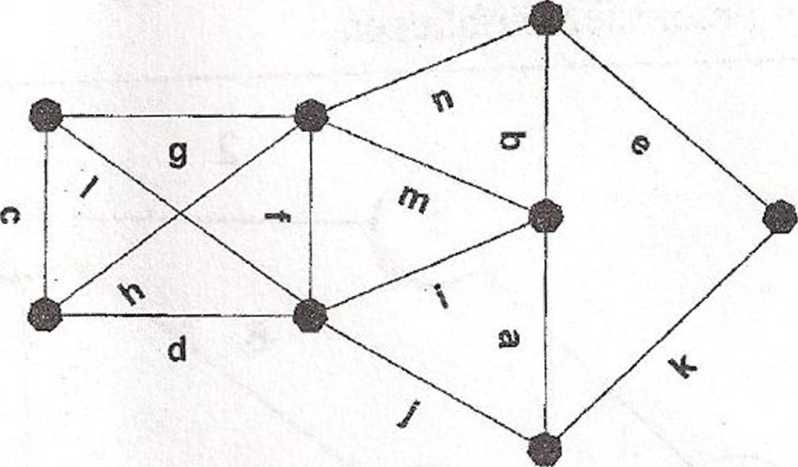
2. (pkt. 2) Na rys. (a) pokazany jest graf z wagami, a na rysunkach (b) i (c) pokazane są dwa różne sposoby oznaczenia etykietami jego krawędzi za pomocą liter a, b, ..., n w kolejności rosnących wag.

(a)    Zastosuj algorytm Kruskala do grafu o krawędziach uporządkowanych tak jak na rys. (b). Narysuj otrzymane minimalne drzewo spinające i podaj jego wagę.

(b)    Powtórz zadanie (a), kiedy krawędzie są uporządkowane tak, jak na rysunku (c).

(b)    (c)

3.    (pkt. 2) Do rozwiązania pewnego zadania algorytmicznego zaproponowano cztery różne algorytmy należące do następujących klas złożoności:

fi (n) = O (n*2^n/2) f₂ (n) = O(n¹⁰°) f₃(n) = O (lg₂n*2ⁿ) f₄(n) = O (2ⁿ)

4.    (pkt. 2) Stosując metodę pierwiastków charakterystycznych rozwiązać równanie rekurencyjne:

i    &n-l ■^‘223._n~2 f    <2 2    2q — 1

5.    (pkt. 3) Załóż, że dla dyskretnego problemu plecakowego przyjęto następujące dane: n = 5 (liczba elementów do upakowania), W = 9 (maksymalny udźwig plecaka), elementy (waga, wartość): (2,3), (3,4), (4,5), (5,6), (6, 7).