Egzamin 12 13

Egzamin z matematyki

Wydział WILiŚ, Budownictwo, sem. 2, r.ak. 2012/2013

ZADANIA

Zad.Zl (9p - rozwiązanie piszemy na stronie 1]

Dane jest pole wektorowe F(x, y> z) = [3 cos x e^v , 3 sin x e^v - 2z sin y , 2 cos y — 3.z²]. Sprawdzić czy pole to jest potencjalne. Jeżeli tak, wyznaczyć, potencjał tego pola. Obliczyć f Fodr , gdzie krzywa L ma parametryzację

L

z(t) = sin2t, y(t) = sin3t, z(t) = sin4i, t e [0, \].

Zad.Z2 [6p - rozwiązanie piszemy na stronie 2]

Obliczyć masę luku l : x(t) = e¹, y(t) = e‘, z(t) = t, t G [0,1], jeżeli g(x₎y,z) — xy.

Zad.Z3 [8p * rozwiązanie piszemy na stronie 3]

⁰⁰ {—l)ⁿ(32 —6)ⁿ

Dany jest szereg potęgowy ]P -. Wyznaczyć promień zbieżności, przedział zbieżność oraz

n=o    yn + 1

zbadać zbieżność szeregu (i określić jej rodzaj) w prawym krańcu przedziału zbieżności.

Zad.Z4 [8p - rozwiązanie piszemy na stronie 4]

Dana jest funkcja f(x) ~ —=— -—. Rozwinąć funkcje f(x) i /'(x) w szereg Taylora w otoczeniu xq = —3.

x^Ł 4- ox + 18

Obliczyć /(⁴⁶*(—3).

Zad.Z5 [9p - rozwiązanie piszemy na stronie 5]

Dana jest gęstość prawdopodobieństwa zm. los. X:

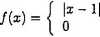
x G [0,2] x i [0,2]

Obliczyć P{ 1 - X² ^ 0). Wyznaczyć dystrybuantę zm. los. X oraz narysować jej wykres. Obliczyć EX, D²X oraz D²(5X -f- I).

Max. 40 pkt

TEORIA

Zad.Tl [5p - rozwiązanie piszemy na stronie 1]

o° j

Podać kryterium całkowe zbieżności szeregu. Korzystając z tego kryterium wykazać zbieżność szeregu Y\

n-i n²

Zad.T2 [5p - rozwiązanie piszemy na stronie 1]

Podać twierdzenie Greena. Korzystając z tego twierdzenia obliczyć

/

(2t 4- y)dx - (x + 2y)dy,

gdzie łulc L jest okręgiem zorientowanym ujemnie o równaniu (a: - l)² + (y + l)² = 4. Zad.T3 [4p - rozwiązanie piszemy na stronie 2]

^{{t) =} 7~+l ^ma

Podać definicję punktu wyprostowania krzywej. Czy krzywa, dla której dla dowonego t punkty wyprostowania.

Zad.T4 [3p - rozwiązanie piszemy na stronie 2]

Zm. los. X ma rozkład Bernoulłiego, gdzie n = 20, p - 0,2. Obliczyć EX, D²X. Podać wzór (nie obliczać) P{X = 2).

Zad.T5 [3p - rozwiązanie piszemy na stronie 3]

Zmienna losowa X ma rozkład jV(2,2). Za pomocą tablic obliczyć P(—1 < X < 3).

Max. 20 pkt