img163

1
1
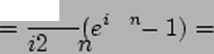
O dla n = ±2, ±4,... ipin dla n = ±1,±3,...
Wyszukiwarka
Podobne podstrony:
8 (32) 158 * dla n = 0, dla n = ±1, ±2,.y.* 8. Pewne funkcje specjalneg. N (60) f(
Przykład: a = 3 jest generatorem £ *7- a° a1 a2 a4 ar 1 3 2 6 4 5 Qp ={1,2,4}
dla formatu A3 — 2,0 Cena opracowania dokumentów w kolorze liczona będzie wg. następujących
rys 2 22 A1 ^ ! A2 - - - D2 PCI AGP _ A1 A2
Przykład c.d. Aksjomaty A1 i A2 wynikają z teorii zbiorów. Aksjomat A3 - łatwo udowodnić Aksjomat
550 XIII. Całki niewłaściwe f ? cos t f J-,n il-y2
piłka nożna 3 Pitka nożna na lekcjach wf B _D °?s; V* X! ®a£i a4 g4 o4 g4 a3®® ® ® ®®x1 A 3® .x, a
5 39 A B C 1 Liczba Moduł 2 159,487 159,487 =MODUŁ.LICZBY(A2) 3 1647,1 1647,1 =MODUŁ.LICZBY(A3)
33913 Plik7 (5) GRAMOFON G-250DANE TECHNICZNE GRAMOFONÓW 220 V lub 110 V, 50 Hz 78±2 obr./min 4
IMG$58 6. Do klasyfikacji wiersza danych: A1 A2 A3 A4 A5 A6 klasa Iow med ? fast i smali
IMG$67 6. Do klasyfikacji wiersza danych: A1 A2 A3 A4 Iow fast smali użyto poniższego drzewa: jakiej
100?16 Równanie Bernoulliego dla przekroju strumienia A1 przed zwężką i dla przekroju strumienia A2
więcej podobnych podstron