0548

550

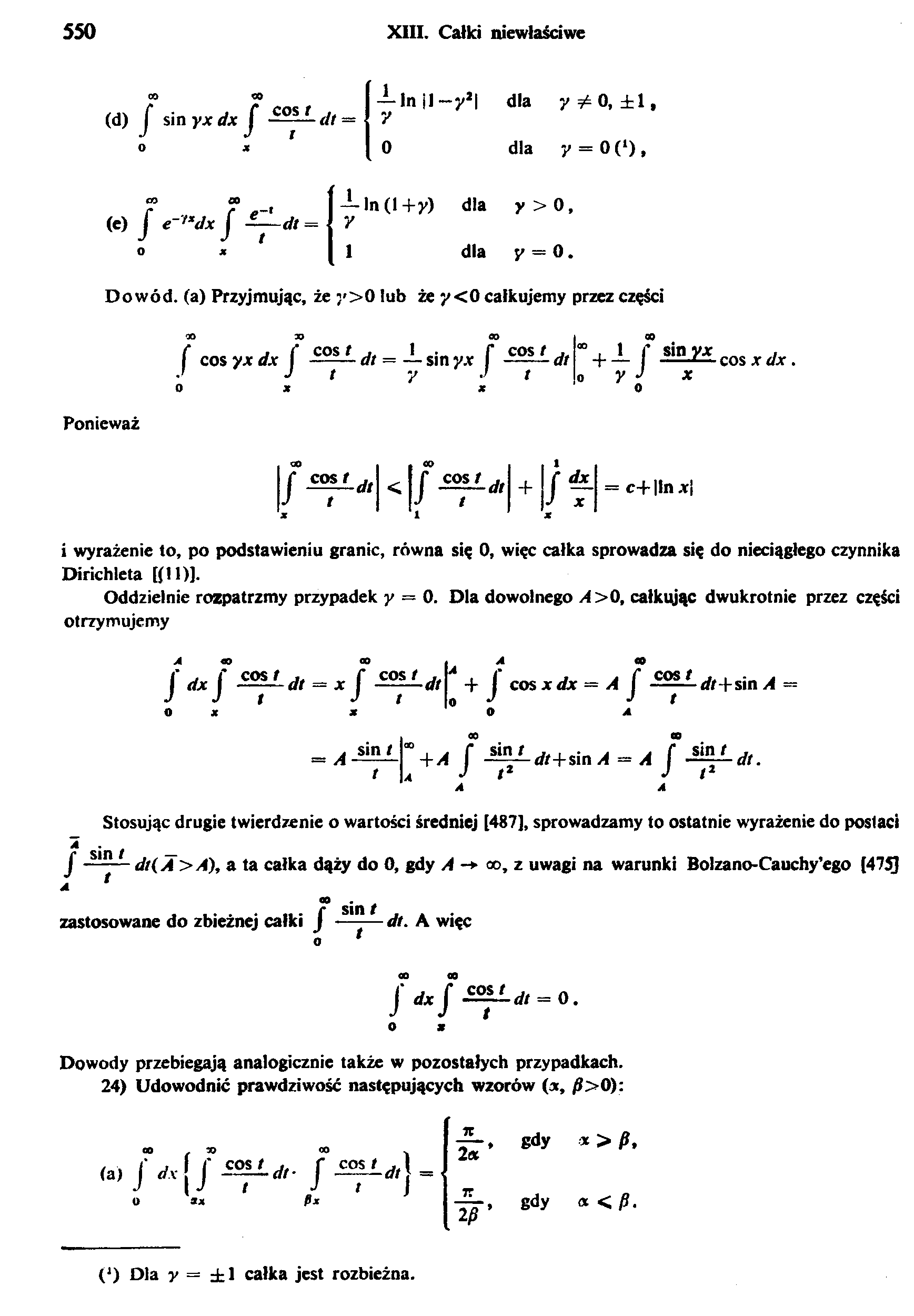
XIII. Całki niewłaściwe

f ? cos t f J-^,n il-y^2| (d) f sinyjcrfjt f --dt — V		dla	y* o, ±1
0 X	0	dla	•/ = 0(‘),
co co (e) j e~^yxdx j ——dt =	— In(l+y) dla /	y	>0,
0 X	1 dla	V	= 0.

Dowód, (a) Przyjmując, że ;’>0 lub że y<O całkujemy przez części

f cosyxdx ( SSLLdt = — sinyx f S£Łl_d,^x + ± f *LZ*_COsxdx. •'    J t    y J t o y J x

Ponieważ

i wyrażenie to, po podstawieniu granic, równa się 0, więc całka sprowadza się do nieciągłego czynnika Dirichleta [(11)].

Oddzielnie rozpatrzmy przypadek y = 0. Dla dowolnego A>0, całkując dwukrotnie przez części otrzymujemy

f _dxf mL_dt = * J ™ŁL_dt +J'_cosxdx = Af S°LL_d,+sinA

⁰ O    A

‘+A f JńLL_dt+sinA = _A fjąL_dt.

J t^z    J t¹

= A

sin t

A    A

Stosując drugie twierdzenie o wartości średniej [487], sprowadzamy to ostatnie wyrażenie do postaci

A .

j —-— dt(A>A), a ta całka dąży do 0, gdy A -*■ oo, z uwagi na warunki Bolzano-Cauchy’ego [475]

OO

zastosowane do zbieżnej całki / —-— dt. A więc

A    *

Dowody przebiegają analogicznie także w pozostałych przypadkach. 24) Udowodnić prawdziwość następujących wzorów (ac, p>0):

—gdy *>P, 2 *

gdy <*</?.

2 P

(') Dla y = ±1 całka jest rozbieżna.