0506

508

XIII. Całki niewłaściwe

iŁ5HL2L . /-JL-N¹ sin** In sin *-*0, 1 lx* \smx J

gdy

*-*0.

Zbieżność.

(d) Przyjmijmy k = sin tu (0<a><ir/2). Punkt osobliwy 0 = <o. Niech znów będzie 0<A< 1; wówczas wyrażenie

In lsin²0—sin²to| l/|0-o>|*

0— to I* sin 0—sin to

|sin 0—sin a>|*{|ln |sin 0—sin co|+ln (sin 0+sin w)}

dąży do zera, gdy 0 -*■ co. Całka jest zbieżna.

i i

3) (a) / *-‘(1-*y-‘*r, (b) / jt-Ul-*)*-¹ lnxdx.

o o

Rozwiązanie, (a) Gdy o<l, punktem osobliwym jest 0, gdy 6< 1 punktem osobliwym jest I. Roz-

1 1/2 i

bijmy daną całkę na dwie, na przykład tak: J = J +/ Ponieważ funkcja podcałkowa jest dla x -*■ 0

O O 1/2

nieskończenie dużą (gdy a<l) rzędu 1—a, więc pierwsza całka jest zbieżna tylko wtedy, gdy 1 —ad, to znaczy gdy a>0. Analogicznie, druga jest zbieżna, gdy b>0. A więc dana całka jest zbieżna wtedy i tylko wtedy, gdy jednocześnie a>0 i 6>0.

1/2

(b) W stosunku do X = 0 nic się nie zmieniło. Wystarczy rozpatrzyć całkę f przy założeniu 1

(dla a>l całka istnieje jako właściwa). Rozumujemy tak samo, jak w przykładzie 3) z ustępu 482. Całka jest zbieżna dla a>0 tak samo jak w przypadku (a).

Natomiast w punkcie x = 1 sytuacja się zmieniła, ponieważ ln x jest dla * -*-1 nieskończenie małą

rzędu pierwszego. Całka f istnieje dla b> — 1.

1/2

Ostatecznie warunki zbieżności danej całki wyglądają tak: a>0, b> — 1.

4)/

sin"~V dfr

11 + k cos ?>|"

Rozwiązanie. Ponieważ przypadek k<0 da się sprowadzić do przypadku k>0 za pomocą podstawienia <p = it—tpt, możemy przyjąć dodatkowe założenie, k>0. Oprócz tego dla zbieżności całki potrzeba w każdym razie, by n>0, bo w przeciwnym razie dla <p -* 0 (lub <p -*■ ir) funkcja podcałkowa jest nieskończenie dużą rzędu >1.

Jeżeli k< 1, to warunek ten jest także dostateczny. Dla k = 1 całka nie może być zbieżna, bo dla tp -*■ jt mamy nieskończenie dużą rzędu 1.

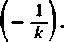
Wreszcie niech będzie k>i. Pojawia się wtedy jeszcze jeden punkt osobliwy <x = arccos

Gdy q> -*■ ot wyrażenie podcałkowe jest nieskończone rzędu n, więc na to, by całka była zbieżna, należy jeszcze zażądać, by było n<l.

A więc całka jest zbieżna, gdy 1) 0<&<1 i n>01ub 2) k>\ i 0<n<l, a w pozostałych przypadkach jest rozbieżna.

oo oo eo

5) (a) f £—dx, (b) f -rr_Tdx, (c) f x’-'e-*dx .

J 1 + * J 1 + a:² J

0 0 0