8 (32)

158

*

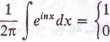
dla n = 0,

dla n = ±1, ±2,.y.*

8. Pewne funkcje specjalne

g. N

(60)    f(xf =    — liczba rzeczywista),

-Ar ■.

która jest w wielu sytuacjach dogodniejsza. Łatwo zauważyć, że każdy wielomian trygonometryczny jest funkcją okresową o okresie 2n.

Jeżeli n jest liczbą całkowitą różną od zera, to e^inx jest pochodną funkcji d**jiri,która jest także funkcją okresową o okresie Dlatego

(61)

Pomnóżmy (60) przez e~^imx, gdzie m jest liczbą całkowitą; całkując ten iloczyn, na mocy

(61)    otrzymamy

(62)    ’    '    c„ = jf(x)e~^,nxdx

przy |m| < N. Jeśli |m| > N, to całka we wzorze (62) jest równa zeru.

Z równości (60) i (62) widać, że wielomian trygonometryczny/określony wzorem (60) jest rzeczywisty wtedy i tylko wtedy, gdy c|j dla n - 0,..., N.

Odpowiednio do (60) szeregiem trygonometrycznym nazywamy szereg o postaci

(63) '    ;    “ X    (^x ~ Kraba fztóywista);^: '

N-ta suma częściowa szeregu jest z definicji równa prawej części równości (60).

Jeżeli /jest funkcją całkowalną na <-n, rc>, to liczby c_m, określone równością (62) dla dowolnej wartości całkowitej m, nazywamy współczynnikami Fouriera funkcji/, a szereg (63) utworzony za pomocą tych współczynników nazywamy szeregiem Fouriera funkcji / Powstaje wobec tego naturalne pytanie: czy szereg Fouriera funkcji/jest do tej funkcji zbieżny lub, ogólniej, czy funkcja/jest przez swój szereg Fouriera jednoznacznie wyznaczona? Mówiąc inaczej, czy znajomość współczynników Fouriera funkcji pozwala ją określić, a jeżeli tak, to w jaki sposób?

Badanie takich szeregów, a w szczególności problem przedstawienia zadanej funkcji w postaci szeregu trygonometrycznego, ma swe źródła w takich działach fizyki jak teoria drgań sprężystych i teoria przewodzenia ciepła (książka Fouriera Analityczna teoria rozchodzenia ąię ciepła była opublikowana w 1822 r.). Wielka liczba trudnych i subtelnych problemów, które powstały przy tych badaniach, spowodowała konieczność przebudowy całej teorii funkcji zmiennej rzeczywistej. Z tymi badaniami związane są nazwiska najznakomitszych matematyków, a wśród nich Riemanna, Cantora i Lebesguea. Można śmiało powiedzieć, że dziedzina ta wraz ze swymi uogólnieniami i rozgałęzieniami zajmuje obecnie centralne położenie w analizie.

Ograni których wj niach natui Początl analogiczni

8.10. D zespolonych

(64)

Wtedy

(65)    *

przy każdyi Na przy tworzą rówi ortonormali

(66)

to liczbę c_n 1 {?>„}. Napisa

tfgjg]

i nazwiemy l Zauważt symbol ten t Podane i pewną własi funkcja feśi

8.11. TW (68)"

będzie n-tą si (69)