044(1)

c) W punktach, w których sin* = O, tj. dla — nn, (n — O, ±1, ±2,

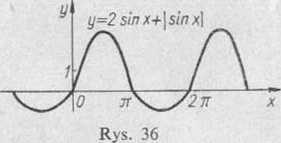
W punktach tych dana funkcja jest nieróżniczkowalna, ponieważ ma ona w tych punktach różne pochodne jednostronne: y’₍-₎ = 1 i y'₍₊₎ = 3 dla n parzystych, oraz y[_-, =' —3 i y[₊₎ = — J dla n nieparzystych. Punkty * = ,v„ są punktami kątowymi wykresu funkcji, gdyż w każdym z tych punktów istnieją po dwie styczne jednostronne o współczynnikach kątowych , i *2 =/(+) (rys. 36).

Wyznaczyć pochodne następujących funkcji:

187. y =

1 '⁴-l

186. y .=

188. w = | cos 4a

190. r = 9; sec² a<p

192. y = ,v⁴(8 ln² w-4 ln x+1)

194. y — ln(.v )-1 .*²+a)

196. u = ln

185. y = (1 + y'w)³

1

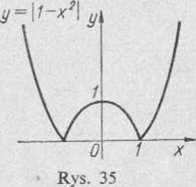
U-*²)³

«189. s = sin⁴ /+cos⁴1 191. .v = 2e^r sin/cos²/

193. u = e²" ln tg ^V-

i

195. .v = In

1 1+A-²

/ Ij-sina \ 1 —sina

2+i 4+5^2jl

197. x = /(cos ln /—sin In /)    198. y

199. y = arc sin [ sin x

201.    y = arc cos (cos w)

202.    y = ^ arc tg x — In

200. r = arc te —¹

9~ 1

203. u = x J 4—.r²+4 arc sin ^ ; obliczyć z/(2)-)-m^,(0)

204*. y = ae~^{sln x}+sin x — 1; wykazać, że y +y cos X = ~ sin 2x

205*. y = 2 cos x |-cos.v; obliczyć y'j-/■ wyznaczyć punkty kątowe wykresu funkcji.

206*. y = x e^x; obliczyć — 1), y'(l) oraz pochodne jednostronne w punkcie kątowym wykresu funkcji.

§ 7. Pochodna logarytmiczna

Różniczkowanie wielu funkcji znacznie upraszcza się, jeśli się je uprzednio zlogarytmuje.

Gdy więc mamy obliczyć y' z równania y = f(x), to można:

a)    zlogarytmować obie strony równania (przy podstawie e)

lny = ln/(x) = ?(*)

b)    zróżniczkować obie strony otrzymanej równości, przy czym traktujemy lny jako funkcję złożoną argumentu x

^V = (f '(x) (zgodnie z wzorem 11)

c)    obliczyć stąd y', czyli y' — y<p'(x). a następnie zastąpić y przez /(.v)

y =/(*) fj’(x)

Pochodną logarytmiczną warto stosować wtedy, gdy dana funkcja zawiera łatwo logarytmujące się działania (mnożenie, dzielenie, podnoszenie do potęgi, wyciąganie pierwiastka), a w szczególności przy wyznaczaniu pochodnej funkcji wykładniczo-potęgowej y = u^v, gdzie u i v są funkcjami argumentu .v.

207. Wyznaczyć pochodne następujących funkcji:

1) y = .v*    2) r = (cosa)⁸*"²*

3) s = —4) R=^(x— 1)] (.v-f l)²(.v —2)

I l-/^:

Rozwiązanie. Stosując metodę wyznaczania pochodnej logarytmicznej znajdujemy kolejno:

91