035(1)

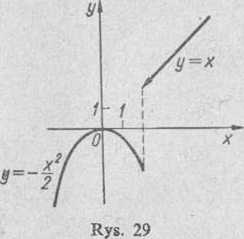
We wszystkich pozostałych punktach osi liczbowej funkcja f(x) jest ciągła, ponieważ obydwa wyrażenia, za pomocą których zadana jest funkcja, określają elementarne funkcje ciągłe. Wykres funkcji pokazano na rys. 29.

2) Nieelementarna funkcja <p(x) jest określona dla wszystkich x > 0. Nieciągłości mogą wystąpić w punktach x = 1 i x — 2,5, w których zmienia się wyrażenie analityczne funkcji. We wszystkich pozostałych punktach swej dziedziny funkcja <f (x) jest ciągła, ponieważ każdy z definiujących ją wzorów określa funkcję elementarną, ciągłą w odpowiednim przedziale zmian argumentu x.

Zbadamy zachowanie się funkcji w punktach x — 1 oraz a^- = 2,5.

a)    x -> 1:

hm <p(x) ■= lim 2 \ x = 2

lim cp(x) - lim (4—2x) = 2 *-»i+o

Zgodnie z warunkiem zadania wartość funkcji <p(x) w punkcie x = 1 jest określona pierwszym wzorem i jest równa

yz (1) = 2 j/F = 2

Zatem w' punkcie x = 1 spełnione są obydwa warunki ciągłości: funkcja jest określona w otoczeniu punktu x = 1 oraz

lim <p(x) = lim ę>(x) = <p(l)

*->■1-0    *-*I+0

czyli funkcja <p(x) jest ciągła w punkcie x = 1.

b)    x -» 2,5:

lim (f (x) = lim (4 — 2x)= — 1

* >2,5—0

lim 9?(x) = lim (2x—7) = —2

*-►2.5 to

W tym przypadku lewo- i prawostronna granice są skończone, ale niejednakowe; nie spełniony jest więc drugi warunek ciągłości. Dlatego w punkcie x = 2,5 funkcja jest nieciągła (nieciągłość skończona).

Skok funkcji w punkcie nieciągłości jest skończony i wynosi

lim <p(x) — lim <p(pc) = — 2—(— 1) = — 1

2,5+0    *->2,5-0

Wykres funkcji przytoczono na rys. 30.

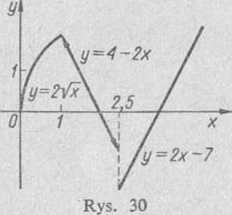
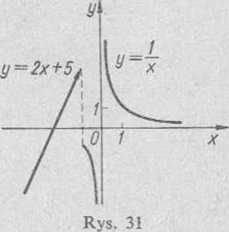
3) Funkcja nieelementarna F(x) jest określona na całej osi liczbowej oprócz punktu x = 0. Oznacza to, że funkcja jest w tym punkcie nieciągła. Badamy zachowanie się funkcji w tym punkcie. Ponieważ dla x -*• —0

zmienna a-jest wielkością ujemną nieskończenie małą, a jest wielkością

ujemną nieskończenie wielką, to

lim F(x) = lim — = — oo *->-o    *

Z kolei dla x -> -)-0 zmienna x jest wielkością dodatnią nieskończenie małą, a wielkością dodatnią nieskończenie wielką, czyli

lim F(x) — lim - - = + oo

1-0    %

Zatem w punkcie x 0 funkcja F{x) ma nieciągłość nieskończoną.

Z kolei badamy zachowanie się funkcji w punkcie = —1, bowiem funkcja F(x) jako funkcja nieelementarna może być także nieciągłą w punkcie, w którym zmienia się jej analityczne wyrażenie. Ponieważ na lewo od punktu x = — 1 funkcja F(x) = 2,v [-5, więc

lim F(.v) = lim (2a-F5) = 3 * *-i-o

69