IMGt43 (2)

148 III. Wstępne wiadomości z rachunku różniczkowego i całkowego'

Funkcja e jest ciągła w punkcie b-f{a\ a funkcja /ciągła w punkcie a, więc limę =fi(b)=0. Wobec tego z równości (11) w granicy dla x-*a dostajemy (10).

Druga część twierdzenia jest wnioskiem z części pierwszej.

Twierdzenie 9. Funkcja F: D-*Y_X x ... x Y_ki F*^{f_x...../_k), jest \różniczkmlnd

w punkcie aeD wtedy i tylko wtedy, gdy wszystkie jej współrzędne f_x, ...,f_ksą różniczkowalne w punkcie a. Przy tym

Funkcja F jest różniczkowalna wtedy i tylko wtedy, gdy są różniczkowalne wszystkie jej współrzędne i wówczas

Dowód. Wystarczy zauważyć, że

F(x)-F(fl) (fi(x)—fi(a) f_k(x)-f_k(a)'

x—a

('

x—a

’)

i powołać się na twierdzenie 4 z § 9.

Ćwiczenia

1. Niech/: (—1; 1 )-*l (zob. § 23, ćwicz. 3) będzie funkcją określoną następująco:

f(x)=(x,x²,.X¹, ...).

Zbadać różniczkowalność funkcji / w punkcie x=0.

2. Rozważmy funkcję /: R-*l określoną następująco:

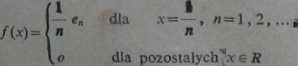
oznaczenia takie jak w ćwicz. 3 z § 23). Dowieść, że funkcja/jest ciągła w punkcie x=*0, nie jest różnicz kowalna w tym punkcie i że styczną do wykresu funkcji / w punkcie (0, /(O)) jest prosta o równanie >**».

unormowane). Dowieść, że jeżeli funkcje/_n ...,/* są różniczkowalne w punkcie a, to funkcja ty: D-*Z gdzie

V(x)=?>(/i(*)> •• ./*(*)),

jest różniczkowalna w punkcie a i

*

t/(a)= jj ę>(/i(a)...../<-i(n),/i'(a),/i₊i(a), ...,/*(a)).

4. Niech Dc.R,f_tj: D-*R^k (1=1,2, k) — funkcje różniczkowalne w punkcie a i yr: B-+R gdzie

^(*)=det [/«(*)!.

Wyznaczyć iy'(a).

Wskazówka. Zob. poprzednie ćwiczenie. Odpowiedź, lf. '(0)=(1, 0, 0, ...).

§ 26. Pochodna funkcji zmiennej rzeczywistej o wartościach rzeczywistych

1. Przykłady. 1. Dla każdego x i dowolnego naturalnego k

(x^ky pip §§

(dla fc=l, x=0 umawiamy się, że 0° = 1).

Dowodzimy tego za pomocą indukcji. Dla k= 1 prawdziwość wzoru, który w tym przypadku przyjmuje postać (x)' = l, wynika wprost z definicji. Zakładając jego słuszność dla pewnego k z równości x^k+1=x^kx wnosimy, że (x^k+l)' =(x^kyx+x^k(xy=fcx^k~^lx+x^k — s(k+l)x^k.

2. Dla x#0 i dowolnego naturalnego k

Na mocy wzoru z poprzedniego przykładu i wzoru (9) z § 25

3. Jeżeli a>0,    1, to dla każdego x>0

(1)

(log_ax)' =-, szczególności (logx)' =

xloga

1

x

Niech x_n>0,‘x„7^tx («== 1,2, ...) i x_n->x. Mamy

log_nx_n-log_flx _    1 log(l+y_n)

. x„-x xloga y_n

gdzie y„= — (x„-x) (n=l,2, ...). Ponieważ y_n>-1 i y„-+0, więc x

log(l+^_n)

y_n

(zob. § 18, wzór (6)) i w takim razie z (2) wynika, że

log_ax_H-log_ax ^    1

x„-x x log 6 *

co dowodzi wzoru (1).

(^ł) (**y oznacza pochodną funkcji x->x* w punkcie x. Symbol f'(x) został zastąpiony znacznie wygodniejszym — chociaż niezbyt poprawnym — oznaczeniem (/(*))'. Tak samo postępujemy w dalszych przykładach.