IMGt47

156 III. Wstępne wiadomości z rachunku różniczkowego i całkowego

156 III. Wstępne wiadomości z rachunku różniczkowego i całkowego

Jeżeli e

= + oo, to f'(x) #0 dla * dostatecznie bliskich x₀ oraz lim (0'(*)//'(x))_ao

więc założenie lim /(x)= +oo implikuje lim (^(x)//(x))*=0. Jeżeli przy tym Iini0(x)*_+fl9

*-**0    X-*X0    X-*Xo

to obie funkcje fi g są dodatnie blisko punktu x₀ i wobec tego lim (/(x)/^(x))s+₀₀

Przypuszczenie, że c=—oo, jest oczywiście sprzeczne z pozostałymi założeniami.

Zastępując w udowodnionej już części twierdzenia / i g odpowiednio przez -fi ~g stwierdzamy, że jest ono prawdziwe także w ostatnim przypadku, gdy wspólną wartością obu granic funkcji / i g w punkcie x₀ jest — oo.

Twierdzenie 8. Niech fg: (a; + co)-*R będą funkcjami różniczkowanymi. Jeżeli g\x)^0 dla każdego x>a oraz

lim /(x)= lim g(x)—0, +oo lub —oo ,

*-* + «

*-* + eo

to z istnienia granicy

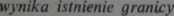
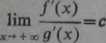
Dowód. Można założyć, że o>0. Niech /j(0=/(l/0» 9i(0=9(^l/0 ^łe@’ Wtedy

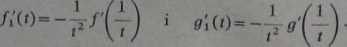
Wobec tego na mocy poprzedniego twierdzenia

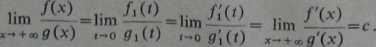
Twierdzenia 7 i 8 znane są pod nazwą reguł de LHospitala.

Ćwiczenia

1. Niech a„eR (/»= 1,2,...),    dla n^m. Przyjmijmy

Wykazać, że /'(*) istnieje wtedy i tylko wtedy, gdy x-ća„ dla im 1,2, ...

Wskazówka. Zastosować twierdzenie 20 z § 23.

2. Dowieść, że funkcja różniczkowalna/: <a; b>-+R jest rosnąca wtedy i tylko wtedy, gdy/'(■*) ^ dla wszystkich x e <a; ó> i zbiór {x : f'(x) > 0) jest gęsty w <a; ó>.

i    11

3, Niech p>0, g > 0,—+—= 1. Dowieść, ze i    P 9i

xy<—x'+—x*    (x>0, y>0).

Wskazówka. Wyznaczyć największą wartość^ funkcji t-+t^I/p—tjp (t>0).

§ 27. Ogólne twierdzenia o przyrostach dla funkcji zmiennej rzeczywistej

1. Problem uogólnienia twierdzeń Lagrange’a i Cauchy ego na przypadek funkcji o wartościach w przestrzeniach unormowanych. Zauważmy, że twierdzenie Lagrange’a o przyrostach nie obowiązuje dla funkcji o wartościach w przestrzeni unormowanej Y^R.

Niech na przykład Y=C i /(x)=cos x+/sin x dla xe <0; 2n>. Ponieważ /(0)=/(2n)=l, więc z twierdzenia Lagrange’a (które w tym przypadku przyjmuje postać twierdzenia Rolle’a) wynikałoby istnienie takiego punktu £, że/'(£)=0. Nie jest to możliwe, bo /'(O" -sin £+/cos ć jest liczbą o module 1.

Twierdzenie Lagrange’a zastępuje twierdzenie o przyrostach w sformułowaniu następującym:

Twierdzenie 1. Niech Y będzie przestrzenią unormowaną. Załóżmy ciągłość funkcji f: <a; b)-+ Y i jej różniczkowalność na (a; b). Jeżeli M^O jest liczbą taką, że

||/^,(^)||^Af dla każdego xe(a;b), to

i|/(6)—/(a)||<Af(h-a).

Udowodnimy twierdzenie ogólniejsze, będące odpowiednikiem twierdzenia Cau-chy’ego:

Twerdzenie 2. Niech Y będzie przestrzenią unormowaną i niech dane będą funkcje ciągle f: (o; by~>Y i g : (a\ by~+R, Jeżeli obie funkcje f i g są różniczkowalne na {a; b) i

§f    11/    dla każdego xe(a;b),

to

I*.    ' \\f(^b)f-f(a)\\^g(b)-g(a).

Aby stąd otrzymać twierdzenie 1, Wystarczy przyjąć g(x)=Mx.

Dowód. Dla danego e>0 niech

U = {xe(a;6): p(x)>0},

gdzie

Z ciągłości funkcji <p wnosimy, | U jest zbiorem otwartym.