IMGt44

ISO 111. Wstępne wiadomości z rachunku różniczkowego i całkowego

Uogólnieniem drugiego ze wzorów (1) jest

... 1

(log mm —— dla x#0.

4. Jeżeli a>0, to dla każdego x

(3)    (fl^x)^,=fl^xlogfl, w szczególności (e^x)' = e^x.

Niech x„#x (n=1,2,...), x_n-+x. Przyjmijmy y_n=a^Xn~^x— 1. Wtedy a^Xn—a^x

(4)

xt    y*

-=a log a-

x_n-x ^g log(l+y_n)

dla n—1,2,... Ponieważ y„> — 1 i y_n-+0, więc tak samo jak w poprzednim przykładzie z (4) wnosimy, że

a^x”-a^x x_n-x

5. Dla dowolnego a i każdego x>0

►A* log a.

(x‘)'=ax^B~¹.

Ponieważ

,    x“=e“^log5C,

więc na mocy wzorów z przykładów 3 i 4 oraz twierdzenia 8 z § 25 o różniczkowaniu złożenia

(x*)'=e'^,0“(ologx)'=e*"“⁵'—

X

6. Dla każdego x

(sinxy=cosx, (cosx)'= — sinx.

Niech x„#x (n=l,2,...), x_n-*x. Mamy

sinx,,—sinx siny,

cos(x+y_B).

cosx„—cosx    siny„

----sin (x+y„),

*»-* y*

, siny,

gdzie y_H=i(Xn-x)->0. Ponieważ ——>1 (zob. § 9, przykład 3) i cos (.x+y_H)^_cos ^ sin (x+y«)-^>sin x wobec ciągłości funkcji trygonometrycznych, więc

sin x_—sin x cos x-—cos x

§ 26. Pochodna funkcji zmiennej rzeczywistej o wartościach rzeczywistych 151

i Wyprowadzimy teraz wzory

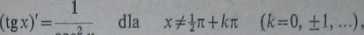
COS X

(ctgx)'=-

dla xźkn (k=0,+1,...).

Na mocy twierdzenia 6 z § 25 o różniczkowaniu ilorazu i wzorów z poprzedniego przykładu

(tgx)'=

(

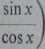
(sin x)' cos x - sin x (cos x)' cos² x+sin² x

Podobnie wyprowadza się drugi wzór.

Zanim przejdziemy do następnych przykładów, udowodnimy następujące

Twierdzenie 1. Jeżeli/: (a; b)-^R jest funkcją ciągłą i ściśle monotoniczną, różniczkowaną w punkcie x e (a; b) i /'(x)#0, to funkcja odwrotna, /^_1 jest różniczkowalna w punkcie y-f(x) oraz

U'^l)\y)=-ż--

WM

Dowód. Zbiór wartości funkcji f będący dziedziną funkcji Z"¹, jest przedziałem. Dla dowolnego ciągu (y_n) punktów tego przedziału, gdzie y_n±y («=1,2,...) i y_n->y, mamy

y,-y

d)

gdzie x„=f~^l(yj) («=1,2,...). Ponieważ funkcja f~^l jest ciągła (zob. § 18, tw. 5), więc ^x^f~^l(y)=x. Stąd i z (5)

f~\y,)-r\y) j |

liii

Następne przykłady ilustrują to twierdzenie. 8. Dla każdego x e (— 1; 1)

(arcsinx)'=-7=, (arccosx)'=—7 == V l-x^2    1 vl-x²

Dla dowodu weźmy jako/w twierdzeniu 1 funkcję x-*sin x zredukowaną do przedziału (~łn;łtt). Otrzymujemy

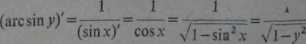
^nigi wzór wyprowadza się zupełnie podobnie.