pochodna funkcji

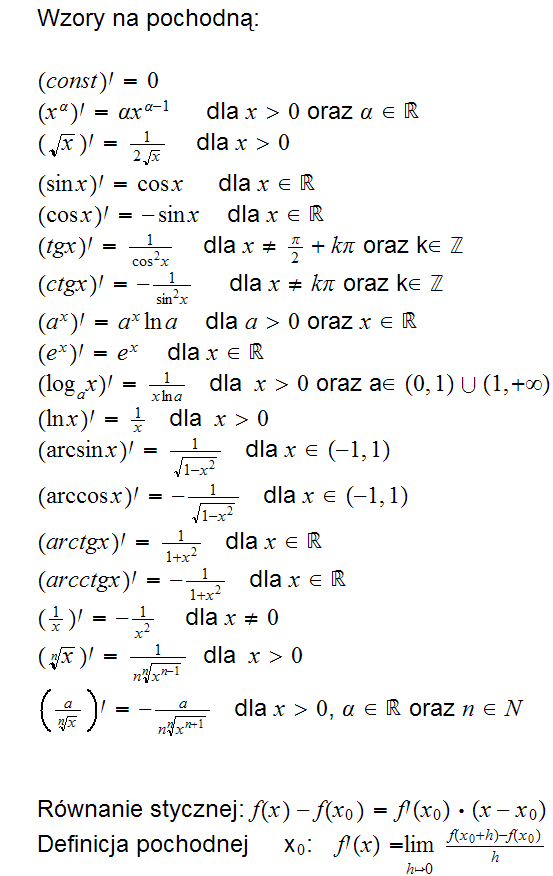
Wzory na pochodną: (consty = 0

(x^ay = ax^a~¹ dla x > 0 oraz a e IE = ^dla*^>0

(sin.r)' = cosr dla igI (cosr)' = -sin.r dla .rei

dlax* f+kn oraz ke Z

(**>' * i

sm~x

(ctgx)' = —7^    dla x * kn oraz ke Z

(a^x)' = a^xlna dla a > 0 oraz rei (e^x)' = e^x dla rei

(log_ar)/ = dla x > 0 oraz ae (0,1) U (l,+°o) (lnr)' = y dla x > 0

(arcsinr)' = (arccosr)' =

_ i

TT?

TT?

dla x e (-1,1) dla r € (-1,1)

(arctgx)> =    dla r e IR

(arcctgx)' = —^l— dla rei (ł)'--+ dla.r*0 ("kć)¹ = i_ dla x > 0

(-*rV = —-y= dla x > 0, a e I oraz n e N

Równanie stycznej:/(r) -/(r₀) = /(r₀) • (r-r₀) Definicja pochodnej x₀: f(x) =lim ^^xo+h)~^Ax°'^>