38517

FAKT: Całka nieoznaczona pochodnej:

Niech funkcja F ma funkcję pierwotną na przedziale I. Wtedy dla każdego xe I zachodzi wzór:

gdzie ce R.

•    Twierdzenie o calkowalności w sensie New tona.

Jeżeli funkcja f(x) jest ciągła na przedziale I, to jest całkowalna w sensie Newtona na tym przedziale.

CAŁKI Z FUNKCJI ELEMENTsiRNYCII

\odx=C

| dx = .r + C

[xⁿdx = —•.r^-*¹ + C./I* -J    /i+ 1

bo

x

n + 1

ln|.r|+ C,.r* 0

[ a^xdx =    — + C,a > 0^A<? * 1,

^J    ln a

a^x V 1    ,

ln a J Ino | e^xdx = e^x + C | sin.rrfr = - cos.v+ C | cos.rrft = sin.r+ C

f —\—dx= - ctgx + C,xt kx .ke C ^J sin^_.x

f —^—dx = tgx + C,x* —+ kx ,ke C * cos* .r    2

f J?* _ = arcsin.x+ C= - arccos.x+ C.|.t|< 1 ¹ yll^x²

[ —-= arctgr + C = - arcctgy + C

ⁱ x" + 1

bo

ln<7 = a'

Przykład: Obliczyć całki:

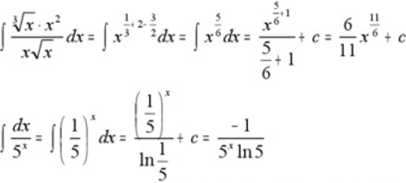
• Twierdzenie o liniowości całki nieoznaczonej: Jeżeli funkcje f i g mają funkcje pierwotne, to:

i) f l/oo i *(*)!<&= | /(*)** | g(.r)*